Собственные колебания без учета сил сопротивления
Уравнение собственных колебаний получим в предположении, что внешние силы и силы сопротивления среды равны нулю.
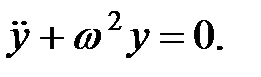
| (1.9) |
Решение уравнения (1.9) известно. Оно имеет следующий вид:
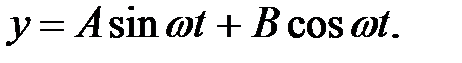
| (1.10) |
Скорость перемещения массы равна:
 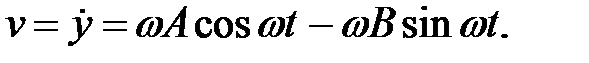
| (1.11) |
Постоянные А и В найдем из начальных условий: при t=0 y=y(0), v=v(0). Подставляя значение t=0 в уравнения (1.9) и (1.11), с учетом начальных условий получаем:
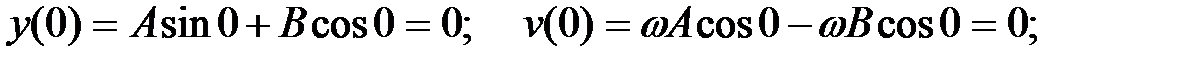
|
Из этих соотношений находим
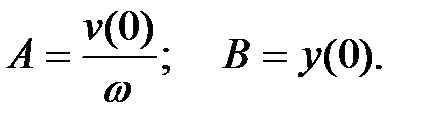
|
Подставляя найденные значения коэффициентов в формулу (9.10), получаем уравнение движения массы при свободных колебаниях:
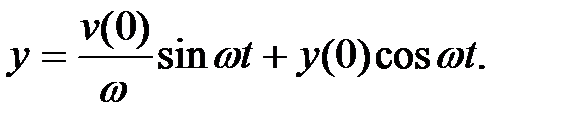
| (1.12) |
Введем новые переменные
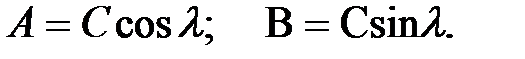
| (9.13) |
Подставив введенные значения коэффициентов в формулу (1.10), получаем
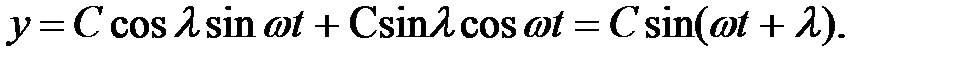
| (1.14) |
Новые коэффициенты, согласно (1.13), равны:
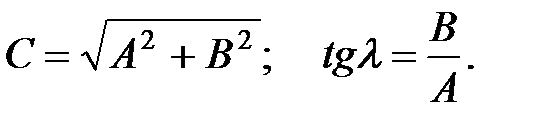
Таким образом, масса совершает гармонические колебания с круговой частотой 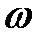 , значение которой находится из формулы (9.6):
, значение которой находится из формулы (9.6):
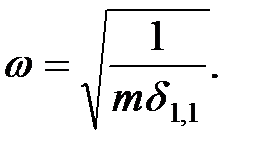
| (1.15) |
Подставив в формулу (1.15) значение m=G/g, где G – вес груза, g – ускорение свободного падения и учтя, что произведение 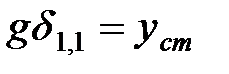 , где
, где 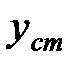 есть перемещение точки присоединения массы от действия груза G, получаем:
есть перемещение точки присоединения массы от действия груза G, получаем:
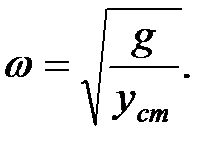
| (1.16) |
Зная круговую частоту собственных колебаний, можно найти период колебаний T и циклическую частоту f из соотношений:
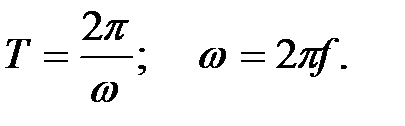
Дата добавления: 2018-03-01; просмотров: 654;
