Собственные колебания с учетом сил сопротивления
Уравнение собственных колебаний с учетом сил сопротивления получим, полагая равной нулю внешнюю силу в уравнении (1).
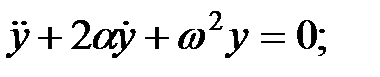
| (1.17) |
Слагаемое 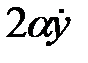 учитывает сопротивление движению: сопротивление внешней среды, трение в местах соединения элементов, внутренне трение (неупругое сопротивление материалов) и т.д. В результате колебания, возникшие под воздействием каких-либо причин, с течением времени затухают (см. рис.1.2). В качестве меры затухания иногда принимают отношение амплитуд колебаний через период
учитывает сопротивление движению: сопротивление внешней среды, трение в местах соединения элементов, внутренне трение (неупругое сопротивление материалов) и т.д. В результате колебания, возникшие под воздействием каких-либо причин, с течением времени затухают (см. рис.1.2). В качестве меры затухания иногда принимают отношение амплитуд колебаний через период 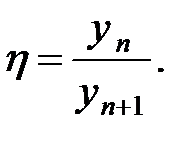 Но чаще в качестве такой меры принимают логарифм этого отношения
Но чаще в качестве такой меры принимают логарифм этого отношения 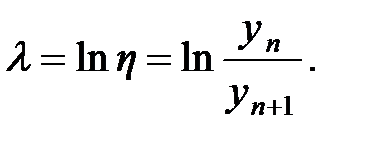

Чтобы найти решение уравнения (9.17), составим характеристическое уравнение:
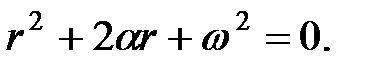
|
Корни характеристического уравнения:
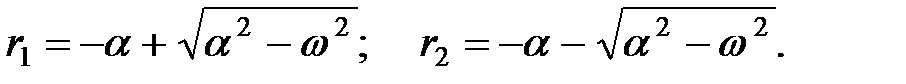
|
Рассмотрим различные случаи.
Характеристическое уравнение имеет комплексно-сопряженные корни; при этом 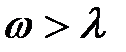 .
.
Корни характеристического уравнения в этом случае равны:
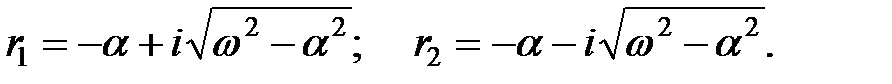
|
Уравнение (1.17) в этом случае имеет следующее решение:
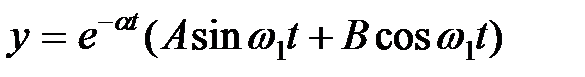 , или , или
| |
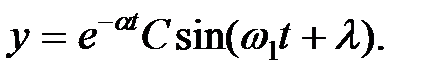
| (1.18) |
График функции (1.18) показан на рис.1.5.
Отношение амплитуд через период равно:
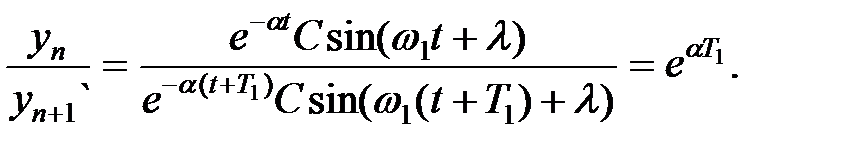
| (1.19) |
Логарифмический коэффициент затухания равен
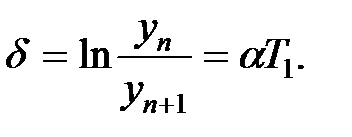
|
Отсюда 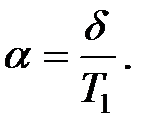 Коэффициент пропорциональности “c” в выражении для силы сопротивления, согласно (1.7) равен
Коэффициент пропорциональности “c” в выражении для силы сопротивления, согласно (1.7) равен
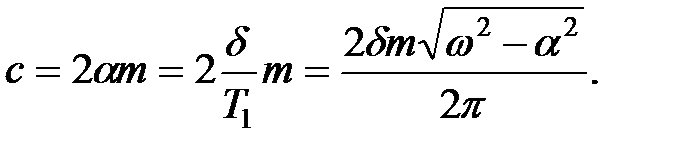
|
На основании проведенных исследований можно сделать следующие выводы:
а) Силы сопротивления уменьшают частоту собственных колебаний.
б) Частота колебаний не зависит от амплитуды.
в) Размахи колебаний с течением времени уменьшаются и колебания затухают.
Корни характеристического уравнения вещественные и разные, при этом  .
.
Корни характеристического уравнения в этом случае равны
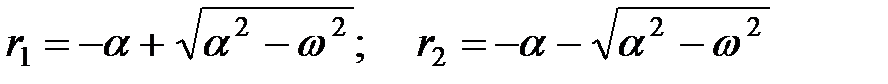 , ,
|
а уравнение (1.17) имеет следующее решение:
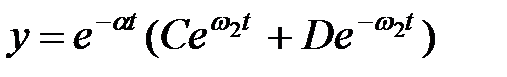
| (1.19) |
Движение конструкции в данном случае оказалось апериодичным. После отклонения конструкции от исходного состояния равновесия она постепенно возвращается к этому состоянию.
Характеристическое уравнение имеет равные корни, при этом 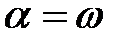 .
.
Корни характеристического уравнения в этом случае равны:
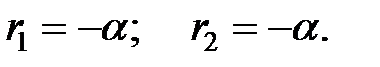
|
Уравнение (1.17) имеет следующее решение:
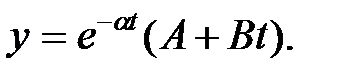
|
И в этом случае движение является апериодическим.
Случаем 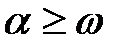 пользуются, когда хотят избежать колебаний.
пользуются, когда хотят избежать колебаний.
Случай, когда 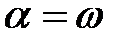 , называют критическим демпфированием. На основании (1.6) коэффициент критического демпфирования
, называют критическим демпфированием. На основании (1.6) коэффициент критического демпфирования 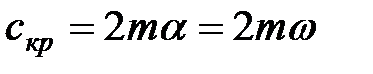 . На практике демпфирование часто задают в долях от критического, т.е. представляют коэффициент демпфирования в виде:
. На практике демпфирование часто задают в долях от критического, т.е. представляют коэффициент демпфирования в виде:
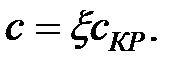
|
Нетрудно выразить коэффициент 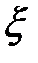 через логарифмический коэффициент затухания, учитывая, что последний определяется формулой
через логарифмический коэффициент затухания, учитывая, что последний определяется формулой 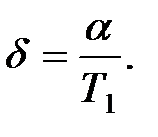
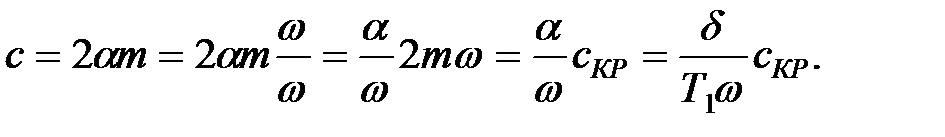
|
Следовательно,
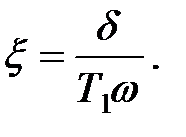
|
Выразим коэффициенты уравнения (1.18) через начальные параметры, т.е. через перемещение и скорость в начальный момент времени (в момент времени t=0).
Находим производную от (1.18):
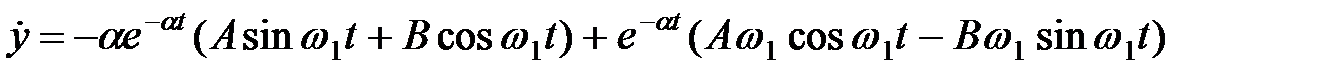 . .
| (1.20) |
Подставляя t=0 в уравнения (1.18) и (1.20) и приравнивая значения перемещения и скорости величинам 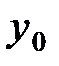 и
и 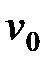 , соответственно, получаем
, соответственно, получаем
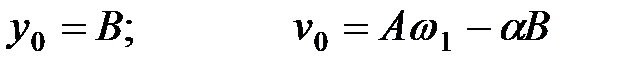 , ,
|
откуда
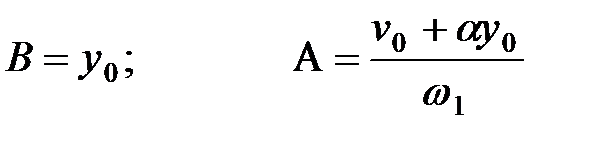 , ,
|
Подставляя найденные значения А и В в уравнение (1.18), получаем
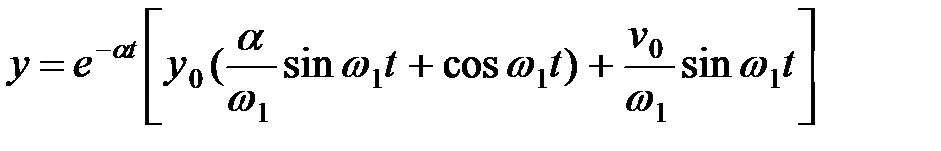 . .
| (1.21) |
ЛЕКЦИЯ 2
Дата добавления: 2018-03-01; просмотров: 773;
