Действие ударной нагрузки на систему с одной степенью свободы
 Пусть на систему с одной степенью свободы падает груз массой m; массу конструкции будем считать пренебрежимо малой по сравнению с массой падающего груза. Требуется найти максимальные значения перемещений и напряжений в конструкции.
Пусть на систему с одной степенью свободы падает груз массой m; массу конструкции будем считать пренебрежимо малой по сравнению с массой падающего груза. Требуется найти максимальные значения перемещений и напряжений в конструкции.
Когда груз коснется конструкции, точка соприкосновения конструкции и груза начнет перемещаться. Кинетическая энергия груза начнет переходить в упругую энергию балки. Когда вся кинетическая энергия перейдет в потенциальную энергию деформации, груз остановится. Перемещение, соответствующее этому состоянию, обозначим 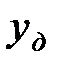 . Запишем уравнение энергетического баланса:
. Запишем уравнение энергетического баланса:
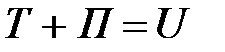
| (1.30) |
где Т – кинетическая энергия бруса в момент соприкосновения, равная 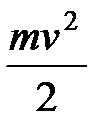 ; П – изменение потенциальной энергии груза, равное
; П – изменение потенциальной энергии груза, равное 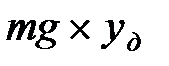 ; U – потенциальная энергия конструкции, равная
; U – потенциальная энергия конструкции, равная 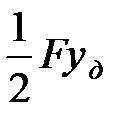 . В выражении для потенциальной энергии F представляет силу, с которой груз действует на балку. Так как
. В выражении для потенциальной энергии F представляет силу, с которой груз действует на балку. Так как 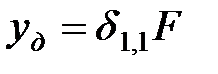 , то
, то 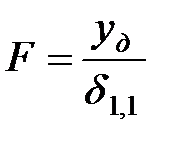 и выражение для потенциальной энергии принимает вид
и выражение для потенциальной энергии принимает вид 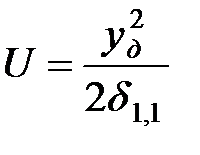 . Подставляя найденные значения в уравнение (1.30), получаем
. Подставляя найденные значения в уравнение (1.30), получаем
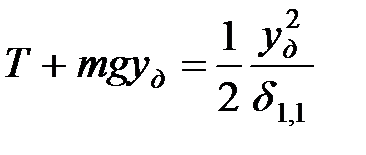
|
или
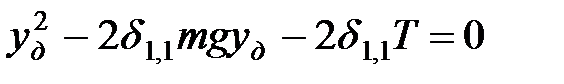 . .
| (1.31) |
Заметим, что произведение 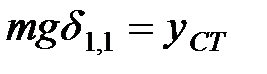 есть статическое перемещение точки соприкосновения под действием веса груза. Тогда
есть статическое перемещение точки соприкосновения под действием веса груза. Тогда
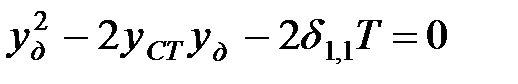
| (1.32) |
Решая уравнение (1.32) относительно 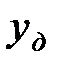 , находим
, находим
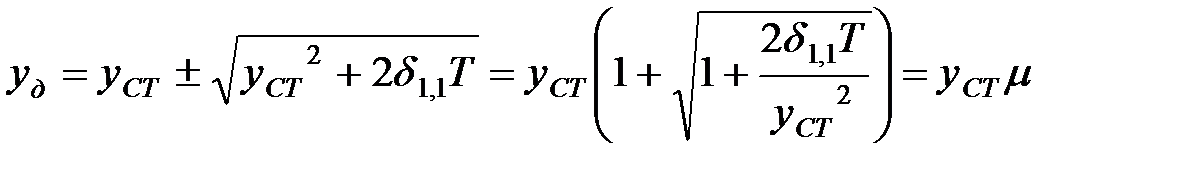 , ,
| (1.33) |
где
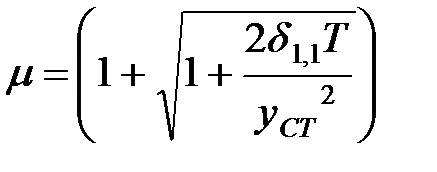
| (1.34) |
есть динамический коэффициент.
Найдем кинетическую энергию в зависимости от высоты падения груза.
Кинетическая энергия в момент соударения равна 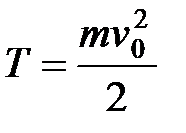 . Со своей стороны
. Со своей стороны 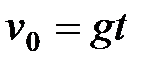 , а
, а 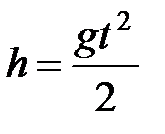 . Тогда
. Тогда 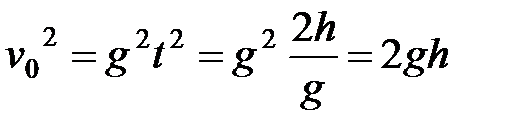 . Следовательно,
. Следовательно, 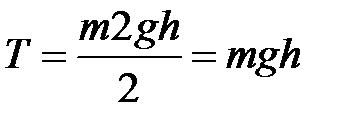 .
.
Подставляя найденное значение Т в соотношение (1.34) получаем
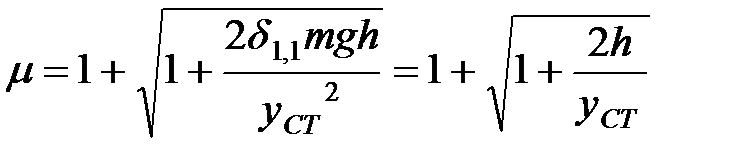
| (1.35) |
Если на конструкции уже имеется масса (рис.1.11), то из 
условия сохранения количества движения 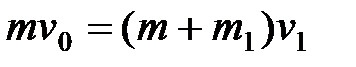 , где
, где 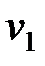 - скорость, с которой обе массы движутся после соударения. Эту задачу можно свести к предыдущей, полагая, что невесомая конструкция подвергается действию массы
- скорость, с которой обе массы движутся после соударения. Эту задачу можно свести к предыдущей, полагая, что невесомая конструкция подвергается действию массы 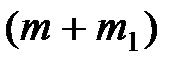 , движущейся со скоростью
, движущейся со скоростью 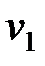 . Тогда в формулу для
. Тогда в формулу для 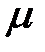 нужно подставить потенциальную энергию
нужно подставить потенциальную энергию
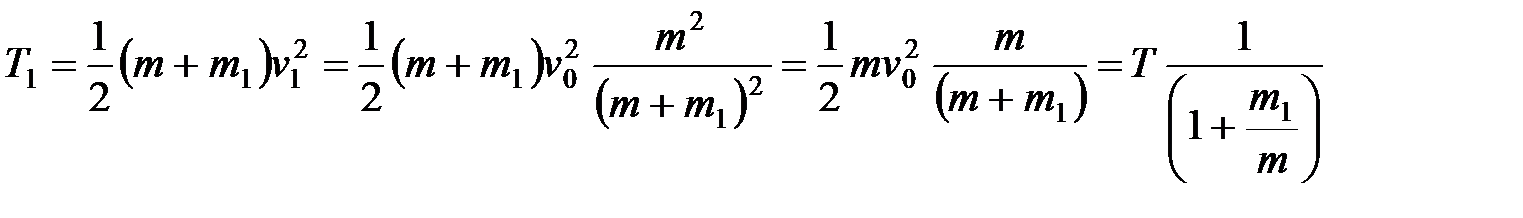 Получаем
Получаем
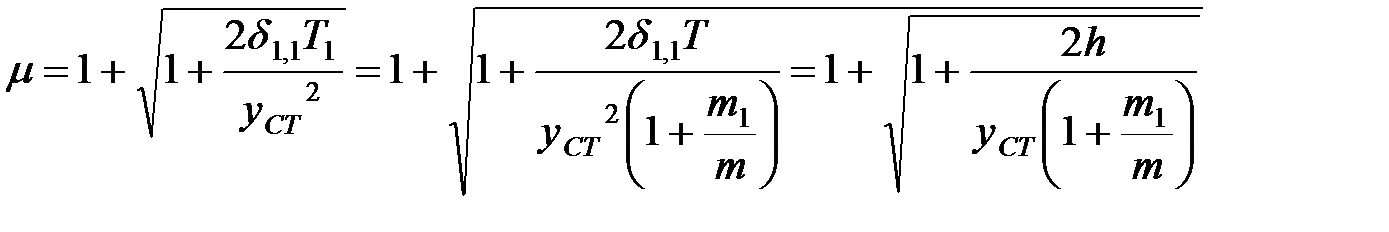
|
Дата добавления: 2018-03-01; просмотров: 639;
