Вынужденные колебания при действии вибрационных сил

Рассмотрим простейший вариант нагружения конструкции, при котором все силы изменяются по гармоническому закону с одной частотой и действуют в одной фазе. При этом все инерционные силы, а, следовательно и перемещения точек и внутренние усилия, будут достигать максимальных значений одновременно. Решим задачу определения этих значений.

Пусть все внешние силы изменяются по закону 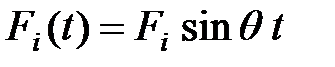. Перемещения и ускорения масс при вынужденных колебаниях с частотой 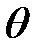определяются так:

.

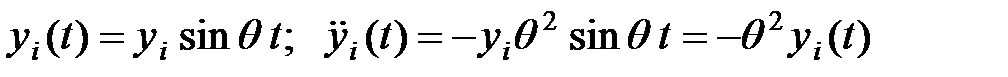Инерционная сила, действующая на 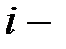ю массу, выражается так: 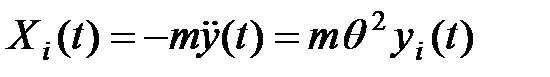. Отсюда

..

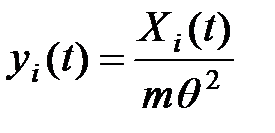(3.6)

Подставляя значения 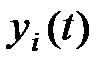из (3.6) в уравнения (3.1), получаем:

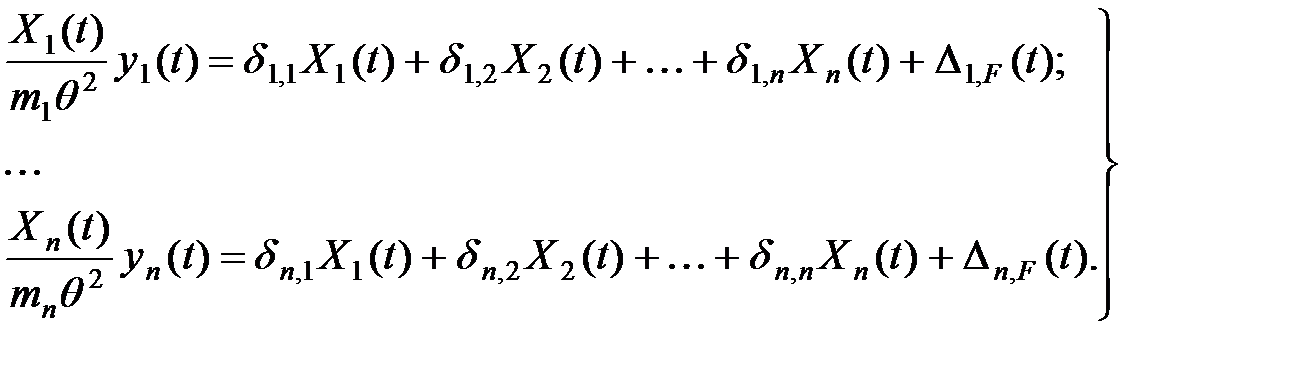
(3.7)

Группируя неизвестные в уравнениях (3.7), приходим к следующей форме этих уравнений:

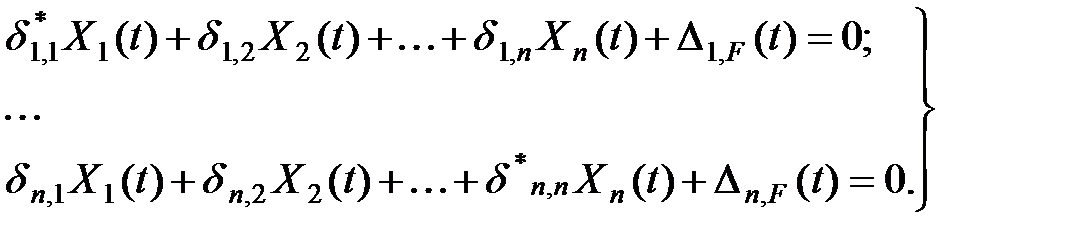
(3.8)

где .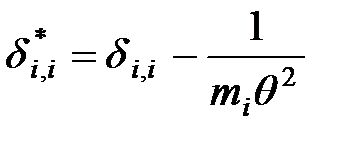

Неизвестные инерционные силы и свободные члены уравнений (3.8) изменяются по гармоническому закону, т.е.

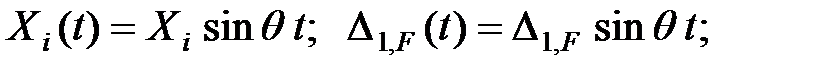
(3.9)

Подставляя значения инерционных сил и свободных членов в уравнения (3.8) и сокращая на 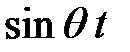, приходим к уравнениям, связывающим амплитудные значения исследуемых величин.

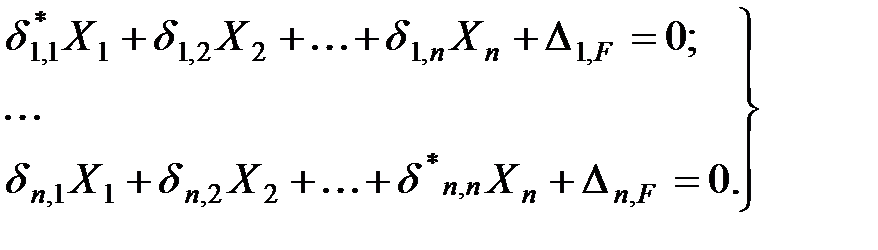
(3.10)

После решения системы уравнений (3.10) и определения амплитудных значений инерционных сил 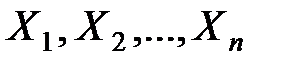эпюра изгибающих моментов строится по формуле

,

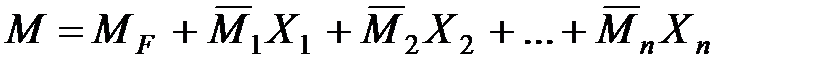где 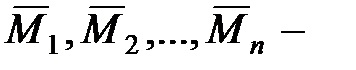изгибающие моменты от единичных сил, приложенных в направлении действия инерционных сил.

Аналогичным образом находятся поперечные и продольные силы в стержнях.