Вынуждение колебания с n-степенями свободы при действии вибрационной нагрузки.

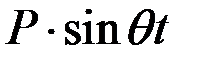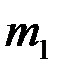Пусть на упругую балку с двумя сосредоточенными массами действует периодическая возмущающая нагрузка гармонического типа (рис. 3). Основная задача расчета заключается в определении максимальных внутренних усилий и перемещений в балке и проверка на резонанс. Перемещения масс и 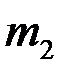от действия инерционных сил и возмущающей нагрузки выражаются следующими зависимостями:

.

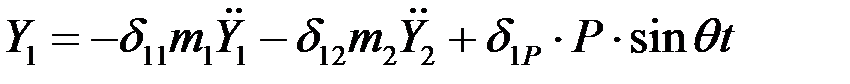
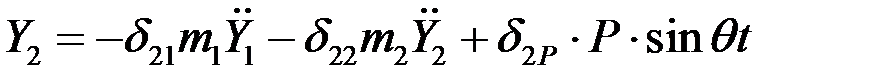или 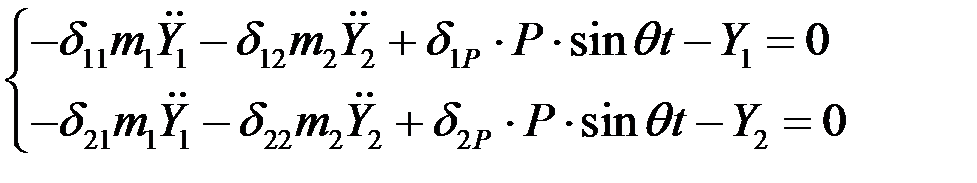(1)

Наличие в уравнениях свободных членов вида 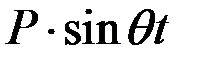дает частый интеграл того же вида, но с иной амплитудой. Будем искать этот частый интеграл в виде:

;

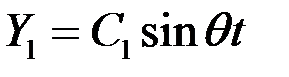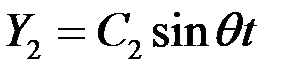
Тогда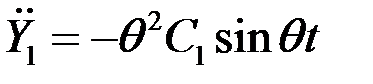

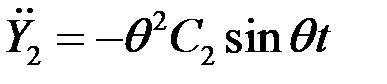
Подставим полученные выражения производных и перемещений в уравнения (1) и сократим на .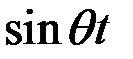

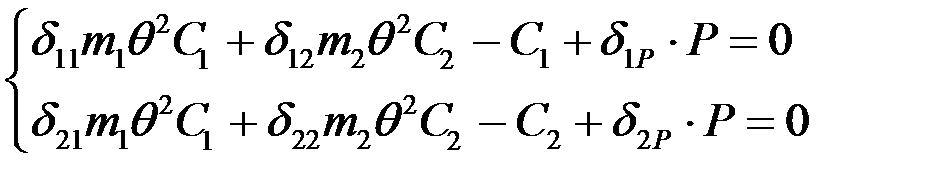
или .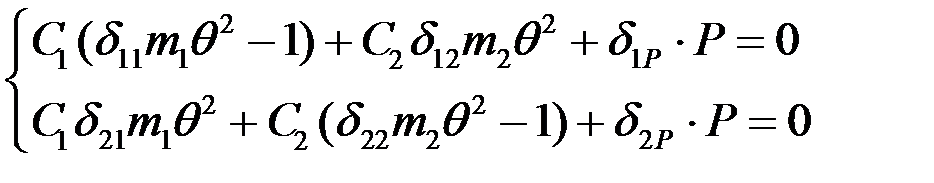

Преобразуем систему уравнений к такому виду 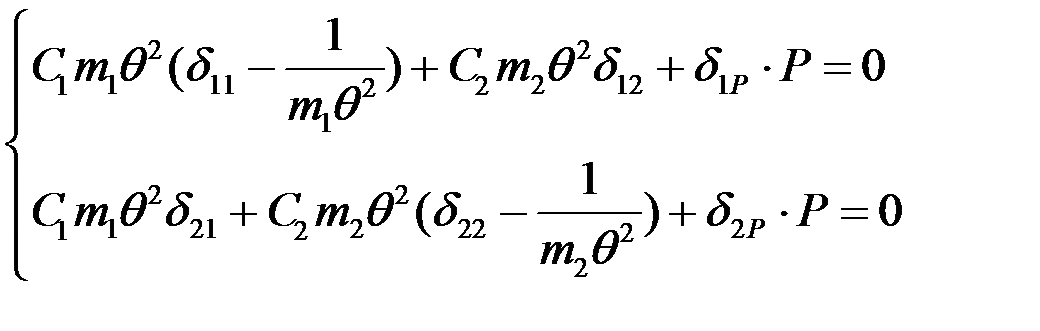(2)

Каждую максимальную амплитуду 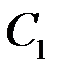и 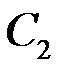можно представить как результат действия максимальных сил инерци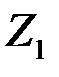и и 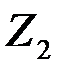и амплитудного значения возмущающей нагрузки .

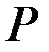Максимальные силы инерции определяются при 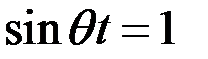, т.е.

,

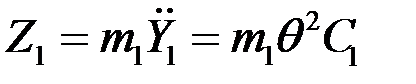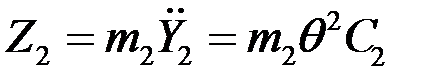
Подставляя в (2) вместо 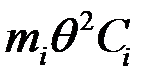величины 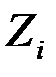, получаем систему канонических уравнений для определения максимальных сил инерции.

.

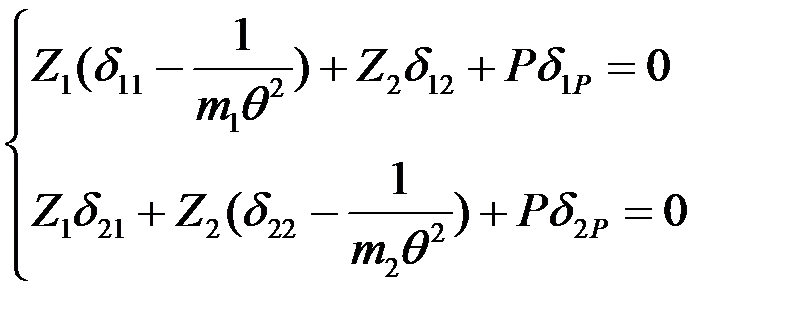Решая эти уравнения при известной частоте возмущений нагрузки, получаем значения максимальных инерционных сил.

В случае, когда частота возмущающей нагрузки 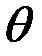совпадает с одной из частот собственных колебаний, наступает явление резонанса.

Зная максимальные силы инерции, можно определить все внутренние усилия в системе в состоянии наибольших отклонений.

,

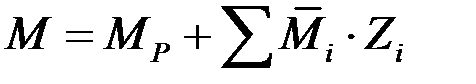
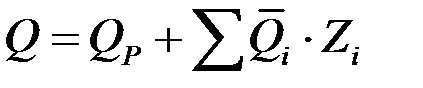
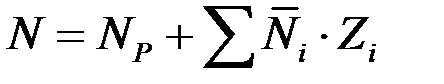где 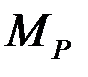, , 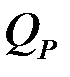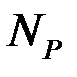– внутренние усилия в системе от действия амплитудного значения возмущающей нагрузки; 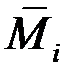, , 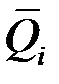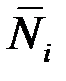– усилия в системе от единичных сил, приложенных по направлению сил инерции.