ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

12. 1. Определение 1.

Сравнением с одной неизвестной называется сравнение по модулю m вида

f(x) º g(x) (mod m) (1), где f(x) и g(x) – многочлены с целыми коэффициентами (целочисленные многочлены), xÎZ, mÎN, m > 1.

В частности, F(x) º0 (mod m) – также сравнение с одной неизвестной. Например,

x² + 2x º x – 1(mod3), 2x³ – 1º0 (mod5) и т. д.

12. 2. Определение 2.

Говорят, что целое число "с" удовлетворяет сравнению (1), если при подстановке числа с вместо х образуется истинное числовое сравнение:

f(с) º g(с) (mod m) – "И" (т.е. истинно).

Например, дано сравнение x² + 2x º x – 1(mod3).

при х = 1: 1² + 2 ×1 º1 – 1(mod3), или 3 º0(mod3) – "И"Þх = 1 удовлетворяет (1);

при х=1+3=4: 4² + 2×4º4 – 1(mod3), или 24º3(mod3) – "И"Þх = 4 удовлетворяет (1).

12. 3. Теорема 1.

Если число "с" удовлетворяет сравнению (1) и с₁ º с (mod m), – то число с₁ также удовлетворяет сравнению (1).

Вывод: если число "с" удовлетворяет сравнению (1), – то класс чисел (вычетов) 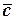по модулю m также удовлетворяет сравнению (1):

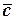= { mq + c / f(mq + с) º g(mq + с) (mod m), qÎZ, – "И" }.

12. 4. Определение 3.

Решением сравнения с одной неизвестной по модулю т называется множество всех классов вычетов по модулю т, удовлетворяющих этому сравнению.

Пример. Решить сравнение 4x º2 (mod6).

Решение.

Существуют 6 классов вычетов по модулю 6: Z₆ = { 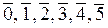}. Составим полную

систему вычетов по модулю 6, например, {0, 1, 2, 3, 4, 5}. Среди них данному сравнению удовлетворяют вычеты 2 и 5 (проверьте!). Значит, решением сравнения будут два класса вычетов: x₁º2(mod6), или x₁=2 + 6q, qÎZ и x₂º5(mod6), или x₂=5 + 6q₁, q₁ÎZ.

Ответ: x₁º2(mod6), x₂º5(mod6).

12. 5. Определение 4.

Два сравнения с неизвестной х по модулю т называются равносильными, если множества их решений совпадают.

12. 6. Теоремы равносильности сравнений с одной неизвестной.

Дано сравнение f(x) º g(x) (mod m) (1). Если:

1⁰ к обеим частям сравнения (1) прибавить один и тот же целочисленный многочлен от х; или

2⁰ обе части сравнения (1) умножить на одно и то же целое число, взаимно простое с модулем т; или

3⁰ обе части сравнения (1) и модуль т умножить на одно и то же натуральное число, – то получим сравнение, равносильное данному.

12. 7. Следствие 1.

а) Можно переносить слагаемые из одной части сравнения в другую с противоположным знаком.

б) Можно все коэффициенты обеих частей сравнения разделить на к, (к, т) = 1.

12. 8. Теорема 2 о замене коэффициентов сравнения.

Пусть даны два сравнения с одной неизвестной:

f(x) = a_n xⁿ + a_{n – 1}x^{n – 1}+ ¼ + a₁x + a₀º0 (mod m), (*)

g(x) = b_n xⁿ + b_{n – 1}x^{n – 1}+ ¼ + b₁x + b₀º0 (mod m). (**)

Если соответствующие коэффициенты a_i и b_i этих многочленов сравнимы по модулю т, то есть если a_i º b_i (mod m) (i = 0, 1, 2, … , n), – то сравнения (*) и (**) – равносильны.

12. 9. Следствие 2.

Если все коэффициенты a_i сравнения (*) заменить числами b_i , сравнимыми с a_i по модулю т, – то получим сравнение (**), равносильное данному.

Пример. 16 х²– 17 х + 10 º0(mod3) Û х²– 2 х + 1 º0(mod3), откуда х º1(mod3).

12.10. Определение 5.

Степенью сравнения (*) называются наибольший показатель степени члена многочлена, коэффициент a_i которого не делится на т.

Пример. Какова степень сравнения 24 х³+ 5 х + 1 º0(mod3) (1) ? Найти его решения.

Решение.

1) По теореме 2 это сравнение равносильно сравнению 5 х + 1 º0 (mod 3) (2) Поэтому данное сравнение – 1-й степени.

2) Для решения сравнения (2) составим классы вычетов по модулю 3: Z₃ = { 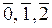} и полную систему вычетов: {0, 1, 2}. Так как х = 0 и х = 2 не удовлетворяют сравнению (2), а х = 1 удовлетворяет ему (проверьте!), – то решением сравнения (2) будет класс вычетов 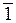, т. е. x = 1 + 3q, qÎZ, или х º1(mod 3). Этот же класс вычетов будет и решением сравнения (1). Ответ: х º1(mod3).

12.11. Теорема 3.

Сравнение п-й степени по простому модулю р ( п < p ) вида

a_n xⁿ + a_{n – 1}x^{n – 1}+ ¼ + a₁x + a₀º0 (mod р), где a_n не 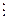р, может иметь не более п классов решений по модулю р.

В частности, при п = 2 сравнение имеет не более двух классов решений. Однако это неверно для составного модуля. Например, сравнение х² – 5х + 6 º0 (mod6) имеет 4 класса решений: х º0, 2, 3, 5 (mod 6) (проверьте!).

ТИПОВЫЕ ЗАДАЧИ

1. С помощью следствий 1 и 2 заменить сравнение

547 х³– 342 х² – 289 х + 782 º434 х³+ 179 х²+ 87 х – 134 (mod3) равносильным сравнением, коэффициенты которого по абсолютной величине были бы меньше модуля.

Решение.

1) По следствию 1 перенесём все члены сравнения в левую часть и приведём подобные члены: 113 х³– 521 х² – 376 х + 916 º0 (mod3).

2) По следствию 2 коэффициенты полученного сравнения заменим числами, сравнимыми с ними по модулю 3 (то есть отбросим слагаемые, кратные трём):

(113 – 111) х³– (521 – 519) х² – (376 – 375) х + (916 – 915) º0 (mod3),

или 2 х³– 2 х² – х + 1 º0 (mod3), или – х³+ х² – х + 1 º0 (mod3),

или х³– х² + х – 1 º0 (mod3).

2. Решить сравнения методом перебора соответствующих классов вычетов.

1) 2 х + 3 º0 (mod8); 2) 6 х³– 7 х² + 13 х – 8 º– 3 х³+ 4 х² + 25 х – 7(mod9).

Решение.

1) Полная система вычетов по модулю 8: {0, 1, 2, 3, 4, 5, 6, 7}. Подставляя в сравнение каждый из этих вычетов, находим, что ни один из них не удовлетворяет сравнению. Значит, данное сравнение не имеет решения.

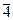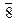2) Упростив данное сравнение (см. задачу 1), получим: 9 х³ – 11 х² –12 х – 1 º0(mod 9) Þ – 2 х² – 3 х – 1 º0(mod 9) Þ 2 х² + 3 х + 1 º0(mod 9). Полная система вычетов по модулю 9: {0, 1, 2, 3, 4, 5, 6, 7, 8}. Подставляя в сравнение каждый из этих вычетов, находим, что сравнению удовлетворяют вычеты 4 и 8. Значит, решением данного сравнения являются классы вычетов и : х º4 (mod 9) и х º8 (mod 9).

Ответ: 1) нет решения; 2) х º4 ;8 (mod 9).