ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

13. 1. Определение 1.

Линейным сравнением с одной неизвестной называется сравнение по модулю m вида ах º b (mod m), где a, b, xÎZ, mÎN, m > 1, а не 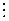т.

13. 2. Техника решения сравнения а х ºb (modm) .

1-й случай: ах º b (mod m), где d = (a; m) = 1.

Тогда сравнение имеет решение и притом единственное (то есть один класс вычетов по модулю т).

Это решение можно найти:

1) способом перебора вычетов из полной системы вычетов по модулю т;

2) использованием теорем равносильности сравнений с неизвестной;

3) по формуле 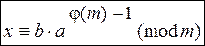(17)

/ см. ниже, Типовые задачи, пример 1 /.

2-й случай: ах º b (mod m), где (a; m) = d ¹ 1, причём b не 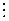d.

Тогда сравнение не имеет решений. / см. ниже, Типовые задачи, пример 2 /

3-й случай: ах º b (mod m), где (a; m) = d ¹ 1, причём b 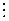d .

Тогда сравнение имеет d классов решений по данному модулю т или 1 класс решений по модулю т : d. / см. ниже, Типовые задачи, пример 3 /

13. 3. Теорема 1.

Всякое сравнение вида ах º b (mod m) равносильно некоторому неопределённому уравнению 1-й степени с двумя неизвестными и целыми коэффициентами вида nx + ky = t ( при некотором условии верно и обратное утверждение).

В самом деле:

1) Дано сравнение ах º b (mod m) Þ (ах – b) 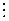m Þ ах – b = mу (уÎZ) Þ ах –mу = b – уравнение 1-й степени.

2) Дано уравнение ах + bу = с, (где а,bÎZ и (а; b) = 1) Þ ах – с = – bу Þ(ах – с) 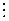b Þ ах º с (mod b) – линейное сравнение.

13. 4. Определение 2.

Тождественным сравнением называется сравнение, которое истинно при любых (целых) значениях неизвестной.

Например: рассмотрим сравнение 6х º 9 (mod 3). При любом х₀ = с Î Z имеем: (6с – 9) 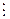3 Þ по лемме 6с º 9 (mod 3) – "И", то есть произвольное число с удовлетворяет данному сравнению, а значит, это сравнение – тождественное.

13. 5. Теорема 2.

Если в сравнении ах º b (mod m) коэффициенты а и b кратны модулю , – то такое сравнение – тождественное.