ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
17. 1. Алгоритм решения сравнений ах º b (mod m), где (а; т) = 1 (18)
В этом случае сравнение (18) имеет 1 класс решений. Для его нахождения нужно:
1) составить дробь 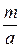 и преобразовать её в конечную цепную дробь:
и преобразовать её в конечную цепную дробь: 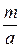 = [a0; a1, a2,…, an]
= [a0; a1, a2,…, an]
2) найти числитель Pп – 1 предпоследней подходящей дроби;
3) применить формулу х º ( – 1) п × b × Рп – 1 (mod m) (19)
(см. ниже, типовые задачи, пример 1 ).
17. 2. Алгоритм решения сравнений ах º b (mod m), где (а; т) =d >1, b  d (20)
d (20)
В этом случае сравнение (20) имеет d классов решений по модулю т. Для их нахождения нужно:
1) сократить a, b и m на число d и получить сравнение (а:d)x º b:d (mod (m:d)) (*)
(чùсла а:d, b:d, m:d – целые!);
2) по алгоритму из пункта 17. 1 решить сравнение (*), имеющее один класс решений по mod (m:d). Получим: x º х0 (mod (m:d)), или x = х0 + (m:d) × t, где tÎZ .
3) полагая число t = 0, 1, 2, … , d – 1, получим d классов решений сравнения (20) по модулю m: x º х0; х0 + (m:d) ×1; х0 + (m:d) ×2; … ; х0 + (m:d) × (d – 1) (mod m) (см. ниже, типовые задачи, пример 2 ).
17. 3. Напомним, что сравнение ах º b (mod m), где (а; т) = d > 1, b не  d, – не имеет решений.
d, – не имеет решений.
ТИПОВЫЕ ЗАДАЧИ
1. С помощью конечных цепных дробей решить сравнение 171 x º3(mod916).
Решение. (См. выше – алгоритм решения – в пункте 17. 1 ).
1) Так как (171;916) = 1 (проверьте!), то сравнение имеет 1 класс решений. Найдём его.
2) Составим дробь 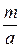 =
= 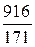 и преобразуем её в цепную дробь:
и преобразуем её в цепную дробь: 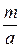 =
= 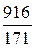 =[5; 2, 1, 4, 12]
=[5; 2, 1, 4, 12]
(см. § 16, типовые задачи, пример 2, в) ).
3) Найдём Pn – 1 – числитель предпоследней подходящей дроби (для проверки вычис-
| лений найдём и Pn ): | ak | 5 2 1 4 12 | Pn – 1 = 75. |
| Pk | 5 11 16 75 916 |
4) Воспользуемся формулой (24) (при п = 4, b = 3, Pn – 1 = 75, т = 916):
х º ( – 1) 4 ×3× 75 (mod916) Þ х º 225 (mod916).
2. С помощью конечных цепных дробей решить сравнение: 42 x º57(mod75).
Решение. (См. выше – алгоритм решения – в пункте 17. 2 ).
1) Так как (42;75) = d =3 (проверьте!) и 57  3, то сравнение имеет 3 класса решений. Сократив a, b и т на d =3, получим сравнение: 14 x º19(mod25). Решим его.
3, то сравнение имеет 3 класса решений. Сократив a, b и т на d =3, получим сравнение: 14 x º19(mod25). Решим его.
2) Составим дробь 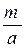 =
= 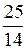 и преобразуем её в цепную дробь:
и преобразуем её в цепную дробь: 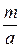 =
= 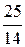 = [1; 1, 3, 1, 2]
= [1; 1, 3, 1, 2]
(проверьте! ); п = 4.
3) Найдём Pn – 1 – числитель предпоследней подходящей дроби (для проверки вычис-
| лений найдём и Pn ): | ak | 1 1 3 1 2 | Pn – 1 = 9. |
| Pk | 1 2 7 9 25 |
4) Воспользуемся формулой ( 24 ) (при п = 4, b = 19, Pn – 1 = 9, т = 25 ):
х º ( – 1) 4 ×19× 9 (mod25) Þ х º 171 º – 4 (mod25), или x = – 4 + 25t,tÎZ.
5) При t =0,1, 2 получим 3 класса решений данного сравнения: х º – 4; 21; 46(mod75).
Дата добавления: 2017-12-05; просмотров: 600;
