ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
14. 1. Определение 1.
| Системой линейных сравнений с одной неизвестной называется система вида | |
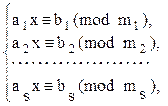
|
где аi , bi., xÎZ, тi Î N. тi >1,
(*) ai не 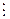 тi (i = 1, 2, ... , s). тi (i = 1, 2, ... , s).
|
14. 2. Определение 2.
Решением системы (*) называется класс вычетов, удовлетворяющий каждому сравнению этой системы.
Если система (*) имеет хотя бы один класс решений, то она называется
совместной (и в противном случае – несовместной).
14. 3. Следствие 1.
Если хотя бы одно из сравнений системы (*) не имеет решений, то и вся система (*) не имеет решений (то есть несовместна).
14. 4. Теорема 1.
| Рассмотрим систему (**)– частный случай системы (*): | |
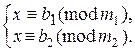 (**) (**)
| Пусть НОД(т1; т2) = (т1; т2) = d, НОК (т1; т2) = [т1; т2] = m. |
Тогда: 1) если (b2 – b1) не  d, то система (**) не имеет решений;
2) если (b2 – b1) d, то система (**) не имеет решений;
2) если (b2 – b1)  d, то система (**) имеет 1 класс решений по модулю [т1; т2] = m. d, то система (**) имеет 1 класс решений по модулю [т1; т2] = m.
|
14. 5. Следствие 2.
Если (т1; т2) = d = 1, – то т = т1 × т2 и система (**) совместна и имеет один класс решений по модулю т = т1 × т2 .
Заметим, что теорема 1 может быть обобщена на случай, когда система (**) содер- жит произвольное (конечное) число сравнений вида x º bj (mod m j).
В частности, если т1, т2 , … , тs – взаимно простые числа, то система (**) всегда совместна и имеет 1 класс решений по модулю т1 × т2 × … × тs .
14. 6. Вернёмся к рассмотрению системы сравнений (*) вида ai x º bj (mod m j).
1) Обозначим (ai ; mi) = di (i = 1, ... , s). Если хотя бы при одном значении i bi не  di,то i-е сравнение системы не имеет решений, а, значит, и вся система (*) несовместна.
di,то i-е сравнение системы не имеет решений, а, значит, и вся система (*) несовместна.
2) Если же bi  di для всех i, то каждое сравнение системы (*) можно решить относительно x и заменить систему (*) равносильной системой (***) :
di для всех i, то каждое сравнение системы (*) можно решить относительно x и заменить систему (*) равносильной системой (***) :
 (***) (***)
| Эта система либо несовместна, либо имеет 1 класс решений по модулю [m1: d1, ... , ms : ds] . |
14. 7. Линейные сравнения по составному модулю вида ax ºb (mod p1 × р2 ).
Так как (ах – b) 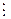 (р1 × р2), то
(р1 × р2), то 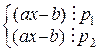 Þ
Þ 
ТИПОВЫЕ ЗАДАЧИ
1. Имеют ли решения системы: 1) 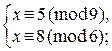 2)
2) 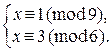 ?
?
Решение.
1) Здесь (т1; т2) = (9;6)= d =3, b2 – b1= 8–5=3.Так как 3  3, то система совместна.
3, то система совместна.
2) Здесь (т1; т2) = (9;6)= d =3, b2 – b1= 3–1=2.Так как 2 не  3, то система несовместна.
3, то система несовместна.
2. Решить систему: 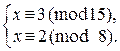
Решение.
1) Выразим х из первого сравнения и подставим во второе:
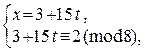 Þ
Þ 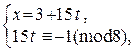 Þ
Þ 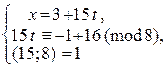 Þ
Þ 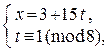 Þ
Þ
Þ 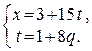
2) Подставим t в 1-е сравнение: x = 3 + 15(1+ 8q) Þ x = 18+120q или х º 18(mod120).
3. Решить систему: 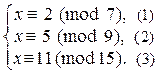 (Здесь т = [7; 9; 15] = 7 ×9 ×5 = 315 ).
(Здесь т = [7; 9; 15] = 7 ×9 ×5 = 315 ).
Решение.
1) Из (1) x = 2 + 7 t, подставим в (2):
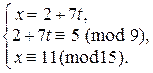 Þ
Þ 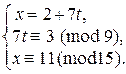 Þ
Þ 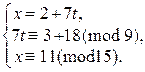 Þ
Þ 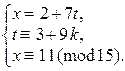 Þ Þ
Þ Þ 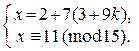 Þ
Þ 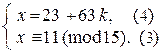
2) Подставим х из (4) в (3):
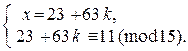 Þ
Þ 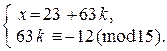 Þ
Þ 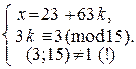 Þ
Þ
Þ 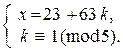 Þ
Þ 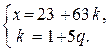 Þ х = 23 + 63 (1 + 5q) Þ x = 86 + 315 q.
Þ х = 23 + 63 (1 + 5q) Þ x = 86 + 315 q.
Ответ: х º 86 (mod 315).
4. Решить систему: 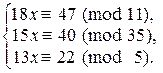 (Здесь т = [11; 35; 5] = 11×35 = 385 ).
(Здесь т = [11; 35; 5] = 11×35 = 385 ).
Решение.
Упростим данные сравнения и решим каждое из них (это возможно – проверьте!).
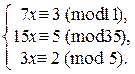 Þ
Þ 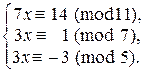 Þ
Þ 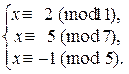 Þ
Þ 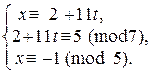 Þ
Þ
Þ  Þ
Þ 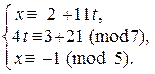 Þ
Þ 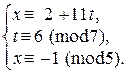 Þ
Þ 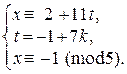 Þ
Þ
Þ 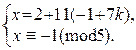 Þ
Þ 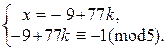 Þ
Þ 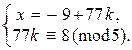 Þ
Þ 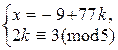 Þ
Þ
Þ 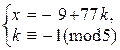 Þ
Þ 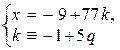 Þ х = – 9 + 77 (– 1 + 5q) Þ х = – 86 + 385 q.
Þ х = – 9 + 77 (– 1 + 5q) Þ х = – 86 + 385 q.
Ответ: х º – 86 (mod 385).
5. Решить линейное сравнение по составному модулю: 5х º 8 (mod 21).
Решение.
Так как здесь модуль 21 = 7×3, то сравнение равносильно системе 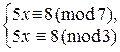 Þ
Þ
Þ 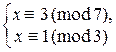 Þ
Þ 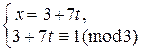 Þ
Þ 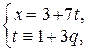 откуда х = 3 + 7(1 + 3q) Þ
откуда х = 3 + 7(1 + 3q) Þ
Þ х = 10 + 21q, или х º 10 (mod 21).
Дата добавления: 2017-12-05; просмотров: 572;
