ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
16. 1. Определение 1.
| Конечной цепной дробью называется число Ап вида | |
Ап = 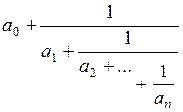 , ,
| где а0Î Z,
аi Î N ( i = 1, 2, . . . , n), аn ¹ 1,
n – длина цепной дроби.
Обозначение: 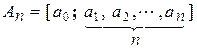
|
Пример конечной цепной дроби: Ап = 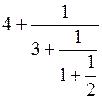 = [4; 3, 1, 2], где n = 3.
= [4; 3, 1, 2], где n = 3.
16. 2. Отметим, что: 1) всякая конечная цепная дробь преобразуется в рациональное
число вида 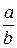 .
.
Например: А3 = [4; 3, 1, 2] = 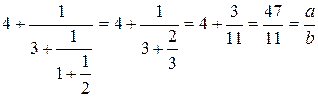 .
.
2) обратно: всякое рациональное число вида 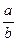 может быть представлено в виде конечной цепной дроби, причём единственным образом..
может быть представлено в виде конечной цепной дроби, причём единственным образом..
16. 3. Алгоритм преобразования несократимой дроби 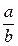 в конечную цепную дробь.
в конечную цепную дробь.
Пример. Дробь 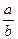 =
= 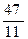 преобразовать в конечную цепную дробь.
преобразовать в конечную цепную дробь.
Решение.
1) Делим числитель 47 на знаменатель 11, остаток r1 = 3;
2) делим знаменатель 11 на 1-й остаток, r1 = 3;
3) делим 1-й остаток r1 = 3 на 2-й остаток, r2 = 2;
4) делим 2-й остаток r2 = 2 на 3-й остаток, r3 = 1;
5) выписываем частные а0 = 4, а1 = 3, а2 = 1, а3 = 2.
Ответ: дробь 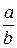 = = 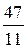 = [4; 3, 1, 2], где n = 3. = [4; 3, 1, 2], где n = 3.
| 47 | 11_ 44 4 = а0 11 | 3 = r1 9 3 = a1 3 | 2 = r2 2 1 = a2 2 | 1 = r3 2 2 = a3 0 |
16. 4. Рассмотрим конечные цепные дроби:
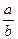 = А3 = [4; 3, 1, 2] =
= А3 = [4; 3, 1, 2] = 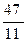 = 4
= 4 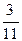 ; А2 = [4; 3, 1] = 4
; А2 = [4; 3, 1] = 4 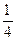 ; А1 = [4;3] = 4
; А1 = [4;3] = 4 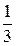 ; А0 = [4] = 4.
; А0 = [4] = 4.
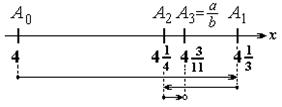
| Числа последовательности А0, А1, А2, А3,… всё ближе подходят к данному числу Ап = а/b. Причём Аi с чётными номерами – слева от Ап, Aj с нечётными номерами – справа от Ап. |
В общем случае:

| Последовательность А0, А2, А4,…возрастает, Последовательность А1, А3, А5,… убывает; члены каждой последовательности всё ближе подходят к исходному числу Ап = а/b. |
| 16. 5. Определение 2. Подходящей дробью k -го порядка данной конечной цепной дроби Ап = а/b называется конечная цепная дробь Аk = [ a0; a1, a2, … , ak] (k £ n), полученная из данной цепной дроби Аn = [ a0; a1, a2, … , ak, …, an] отбрасыванием последних n – k чисел. |
Пусть 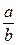 – несократимая дробь. Если
– несократимая дробь. Если 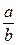 = Аn = [ a0; a1, a2, …, an], то
= Аn = [ a0; a1, a2, …, an], то
А0 = [ a0] – подходящая дробь 0-го порядка;
А1 = [ a0; a1] – подходящая дробь 1-го порядка;
А2 = [ a0; a1, a2] – подходящая дробь 2-го порядка;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Аn = [ a0; a1, a2, …, an] – подходящая дробь п-го порядка.
Обозначение k-й подходящей дроби: 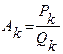 , где Pk – числитель k-й подходящей дроби,
, где Pk – числитель k-й подходящей дроби,
Дата добавления: 2017-12-05; просмотров: 532;
