ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

10. 1. Теорема Паскаля (1623 – 1662).

Даны натуральные числа: т > 1 и n, записанное в t - ичной системе:

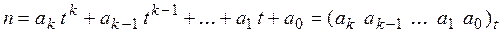, где a_i – – цифры: a_i ÎN, 0 £ a_i £ t –1 (i = 0,1, 2,…, k ), tÎN, t > 1.

Пусть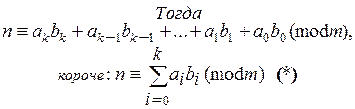

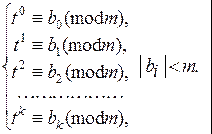
Итак: из равенства (*) в теореме Паскаля следует, что число n и число 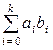сравнимы по модулю т (а значит – равноостаточны при делении на т). Отсюда, в частности, вытекает, что если 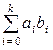делится на т без остатка, то и n делится на т без остатка. Поэтому имеет место следствие:

10. 2. Следствие.

Для того, чтобы число n делилось без остатка на число т, необходимо и достаточно, чтобы сумма 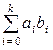делилась без остатка на т:

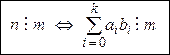(16)

ТИПОВЫЕ ЗАДАЧИ

1. Установите в десятичной системе счисления признаки делимости на 3, на 9 и на 11.

1) Признаки делимости на 3 и на 9.

Пусть n = (a_k a_{k – 1} … a₁ a₀)₁₀ = a_k ×10^k +a_{k – 1}×10^{k – 1}+…+a₁×10 + a₀, m =3 и m = 9.

1) Найдём b_i : по модулю m = 3по модулю m = 9

10⁰ º1(mod3), т.е. b₀ =1, 10⁰ º1(mod9), т.е. b₀ =1,

10¹ º1(mod3), т.е. b₁ =1, 10¹ º1(mod9), т.е. b₁ =1,

10² º1(mod3), т.е. b₂ =1, 10² º1(mod9), т.е. b₂ =1,

¼¼¼¼¼¼¼¼¼¼ ¼¼¼¼¼¼¼¼¼¼

10^k º1(mod3), т.е. b_k =1, 10^k º1(mod9), т.е. b_k =1,

¼¼¼¼¼¼¼¼¼¼ ¼¼¼¼¼¼¼¼¼¼

2) Составим сумму 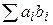. В обоих случаях сумма 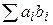= = 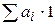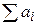(сумме

цифр числа n).

3) Из (16) следует : число n делится на 3 тогда и только тогда, когда сумма цифр числа n делится на 3.

Аналогично: n 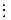9 Û (сумма цифр числа n ) 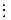9.

2) Признак делимости на 11.

1) Найдём b_i по модулю m = 11: 10⁰ º1(mod11), т.е. b₀ = 1,

10¹ º – 1(mod11), т.е. b₁ = – 1.

10² º1(mod11), т.е. b₂ = 1, 10³ º – 1(mod11), т.е. b_п = – 1,

¼¼¼¼¼¼¼¼¼¼

2) Составим сумму 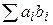= a₀ ×1 + a₁ × ( – 1) + a₂ ×1 + a₃ × ( – 1) + … =

= (a₀ + a₂ + a₄ + …) – (a₁ + a₃ + a₅ + …) = 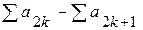(k = 0, 1, 2, 3, …). 3) Из (16) следует: n 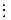11 Û ( 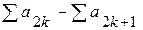) 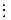11, то есть число n делится на 11

тогда и только тогда, когда разность между суммой цифр числа n , стоящих на чётных местах, и суммой цифр числа n, стоящих на нечётных местах, делится на 11.

Пример. n = 57 926. 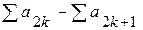= (2 + 7) – (6 + 9 + 5) = 9 – 20 = – 11. Так как – 11 делится на 11, то и число n = 57 926 делится на 11.

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

160. Проверьте справедливость теоремы Паскаля для числа n = a₀+ a₁t + a₂t² + ...+ a_k t^k (t - основание системы счисления, a_i - цифры числа n в этой системе) и модуля m, если: а) n = 1999, m = 7; б) n = 758, m = 5; в) n = 2546, m = 6; г) n = 2546, m = 12.

161. Выведите признак делимости в десятичной системе счисления:

а) на 3; б) на 9; в) на 4; г) на 11; д) на 7; е) на 27; ж) на 101.

162. С помощью соответствующих признаков делимости, полученных в предыдущей задаче, установите, делится ли данное число n на число m (все числа даны в десятичной системе):

а) 5378 на 3; б) 236 484 на 9; в) 15 928 на 4; г) 37 585 на 11; д) 4 859 371 на 11; е) 37 394 на 7; ж) 61 153 701 на 7; з) 37 272 698 на 7;

и) 144 343 на 27; к) 28 657 341 на 27; л) 4 572 573 на 101; м) 32943577 на101.

163. Выведите признак делимости на 4 в 8-ричной системе счисления.

164. Выведите признак делимости на 3 в 5-ричной системе счисления.

165. Выведите признак делимости на 8 в 14-ричной системе счисления.

166. С помощью соответствующих признаков делимости, полученных в предыдущих задачах 163 - 165, установите, делится ли данное число n на число m (оба числа записаны в t-ичной системе). Сделайте проверку непосредственным делением.

а) n = (1 7 5 4) ₈ на m = (4) ₈ ; б) n = (4 1 3 0 2 3 1) ₅ на m = (3) ₅ ; в) n = (3 7 1 4 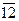)₁₄ на m = (8) ₁₄ .

Глава 4. СРАВНЕНИЯ С ОДНОЙ НЕИЗВЕСТНОЙ

ПО ДАННОМУ МОДУЛЮ

§ 12. ОСНОВНЫЕ ПОНЯТИЯ. РАВНОСИЛЬНОСТЬ СРАВНЕНИЙ