ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
9. 1. Установим условия, при которых число вида 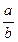 , где а, b Î N, (а, b) =1, а < b, преобразуетсяв тот или иной вид систематической дроби (для случая, когда t = 10, то есть в десятичной системе счисления).
, где а, b Î N, (а, b) =1, а < b, преобразуетсяв тот или иной вид систематической дроби (для случая, когда t = 10, то есть в десятичной системе счисления).
Пусть t = 10 = 2×5, а в числе 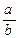 знаменатель b имеет вид:
знаменатель b имеет вид:
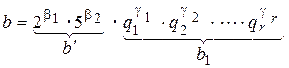 (qi – простые числа), то есть b = b' × b1 Тогда:
(qi – простые числа), то есть b = b' × b1 Тогда:
I Если знаменатель b = b' (содержит только "2" и / или "5"), – то дробь 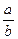 преобразуется в конечную десятичную дробь. Количество десятичных знаков равно наименьшему натуральному числу l, удовлетворяющему сравнению 10 l º 0(mod b' ).
преобразуется в конечную десятичную дробь. Количество десятичных знаков равно наименьшему натуральному числу l, удовлетворяющему сравнению 10 l º 0(mod b' ).
II Если знаменатель b = b1 (не содержит "2" и "5"), – то дробь 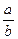 преобразуется в бесконечную чисто периодическую десятичную дробь. Длина периода равна наименьшему натуральному числу k, удовлетворяющему сравнению 10 k º 1(mod b1).
преобразуется в бесконечную чисто периодическую десятичную дробь. Длина периода равна наименьшему натуральному числу k, удовлетворяющему сравнению 10 k º 1(mod b1).
III Если знаменатель b = b' × b1 (содержит "2" и / или"5", а также иные простые множители), – то дробь 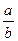 преобразуется в бесконечную смешанную периодическую деся-
преобразуется в бесконечную смешанную периодическую деся-
тичную дробь.
Длина периода равна наименьшему натуральному числу k, удовлетворяющему сравнению 10 k º 1(mod b1 ).
Длина предпериода равна наименьшему натуральному числу l, удовлетворяющему сравнению 10 l º 0(mod b' ).
9. 2. Выводы.
| a | ↗ | к о н е ч н а я д е с я т и ч н а я д р о б ь |  
| рацион.
число 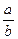 иррацион. число
иррацион. число
| ||
| ↘ | бесконечная десятичная дробь | 
| 1) чисто периодическая дробь 2) смешанная периодич. дробь 3) непериодическая дробь | |||
9. 3. Отметим, что:
рациональным числом является всякая конечная десятичная дробь или бесконечная периодическая десятичная дробь;
иррациональным числом является всякая бесконечная непериодическая десятичная дробь.
ТИПОВЫЕ ЗАДАЧИ
1. Данные обыкновенные дроби, записанные в десятичной системе, преобразовать в
десятичные, предварительно определив вид искомой дроби (конечная или бесконечная; периодическая или непериодическая; если – периодическая, то чисто периодическая или смешанная периодическая); в последних случаях – предварительно найти число k – длину периода и число l – длину предпериода. 1) 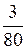 ; 2)
; 2) 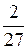 ; 3)
; 3) 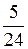 .
.
Решение.
1) У дроби 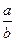 =
= 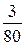 знаменатель – число b = 80 = 24 × 5 содержит только "2" и "5". Поэтому данная дробь преобразуется в конечную десятичную дробь. Количество десятичных знаков l наим определяется из условия: 10 l º0(mod80):
знаменатель – число b = 80 = 24 × 5 содержит только "2" и "5". Поэтому данная дробь преобразуется в конечную десятичную дробь. Количество десятичных знаков l наим определяется из условия: 10 l º0(mod80):
| Имеем:10 1º10(mod80), 10 2= 100 º20(mod80), 10 3º200 º 40(mod80), 10 4º400 º 0(mod80). | Следовательно, l наим = 4, то есть искомая десятичная дробь будет иметь 4 десятичных знака.
Проверка: разделим "уголком" 3 на 80 и получим:
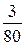 = 0, 0375. = 0, 0375.
|
2) У дроби 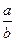 =
= 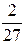 знаменатель – число b = 27 = 33 не содержит "2" и "5". Поэтому данная дробь преобразуется в бесконечную чисто периодическую десятичную дробь. Длина периода k наим определяется из условия: 10 k º1(mod27):
знаменатель – число b = 27 = 33 не содержит "2" и "5". Поэтому данная дробь преобразуется в бесконечную чисто периодическую десятичную дробь. Длина периода k наим определяется из условия: 10 k º1(mod27):
| Имеем: 10 1º10(mod27), 10 2º100–81º19(mod27), 10 3º190 º190 – 7×27 º º 190 – 189 º 1(mod27). | Следовательно, k наим = 3, то есть в искомой десятичной дроби будет период длиной k = 3.
Проверка: разделим "уголком" 2 на 27 и получим: 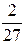 = 0, (074). = 0, (074).
|
3) У дроби 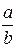 =
= 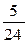 знаменатель – число b = 24 = 23 ×3, то есть имеет вид: b = b' × b1 (кроме "2" или "5" содержит и иные множители, в данном случае число 3). Поэтому данная дробь преобразуется в бесконечную смешанную периодическую десятичную дробь. Длина периода k наим определяется из условия: 10 k º1(mod3), откуда k наим = 1, то есть длина периода k = 1. Длина предпериода l наим определяется из условия: 10 l º0(mod8), откуда l наим = 3, то есть длина предпериода l = 3.
знаменатель – число b = 24 = 23 ×3, то есть имеет вид: b = b' × b1 (кроме "2" или "5" содержит и иные множители, в данном случае число 3). Поэтому данная дробь преобразуется в бесконечную смешанную периодическую десятичную дробь. Длина периода k наим определяется из условия: 10 k º1(mod3), откуда k наим = 1, то есть длина периода k = 1. Длина предпериода l наим определяется из условия: 10 l º0(mod8), откуда l наим = 3, то есть длина предпериода l = 3.
Проверка: разделим "уголком" 5 на 24 и получим: 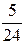 = 0, 208 (3).
= 0, 208 (3).
Ответ: 1) 0, 0375; 2) 0, (074); 3) 0, 208 (3).
Дата добавления: 2017-12-05; просмотров: 435;
