ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

6. 1. Определение 1.

Классом чисел по данному модулю т называется множество всех тех и только тех целых чисел, которые при делении на т имеют один и тот же остаток r, то есть сравнимых по модулю т (т ÎN, т > 1).

Обозначение класса чисел, имеющих остаток r: .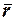

Каждое число из класса 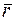называется вычетом по модулю т, а сам класс 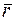называется классом вычетов по модулю т.

6. 2. Свойства множества классов вычетов 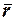по модулю т:

1) всего по модулю т будет т классоввычетов: Z_т = { , , , … , };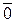

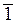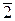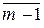2) каждый класс 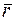содержит бесконечное множество целых чисел (вычетов) вида: 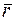= {a = mq + r / qÎZ, 0£ r < m}

3) "а Î 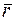: а º r (mod m);

4) "а, b Î 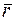: а º b (mod m), то есть любые два вычета, взятые из одного класса, сравнимы по модулю т;

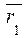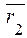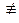5) "а Î , "b Î : а b (mod m), то есть никакие два вычета; взятые из разных классов, несравнимы по модулю т.

6. 3. Определение 3.

Полной системой вычетов по данному модулю т называется любой набор т чисел, взятых по одному и только по одному из каждого класса вычетов по модулю т .

Пример: если m = 5, то {10, 6, – 3, 28, 44} – это полная система вычетов по модулю 5 (причём, не единственная !)

В частности,

множество {0, 1, 2, 3, … , m –1} – это система наименьших неотрицательных вычетов;

множество {1, 2, 3, … , m –1, т}– это система наименьших положительных вычетов.

6. 4. Отметим, что:

если {х₁, х₂, … , х_т} – полная система вычетов по модулю т, то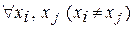

.

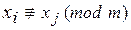6. 5. Теорема 1.

Если {х₁, х₂, … , х_т} – полная система вычетов по модулю т, "а, b Î Z и (а, т) = 1, – то система чисел {ах₁ + b, ах₂ + b, … , ах_т+ b}также образует полную систему вычетов по модулю т .

6. 6. Теорема 2.

Все вычеты одного и того же класса вычетов по модулю т имеют с числом т один и тот же наибольший общий делитель: "а, b Î 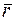Þ (а; т) = (b; т).

6. 7. Определение 4.

Класс вычетов 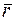по данному модулю т называется взаимно простым с модулем т, если хотя бы один вычет этого класса – взаимно простой с т.

Заметим, что в этом случае по теореме 2 все числа этого класса будут взаимно простыми с модулем т.

6. 8. Определение 5.

Приведённой системой вычетов по данному модулю т называется система вычетов, взятых по одному и только по одному из каждого класса, взаимно простого с модулем т .

6. 9. Отметим, что:

1) приведённая система вычетов по модулю т содержит j(т) чисел {х₁, х₂,…, };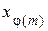

2) : .

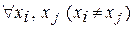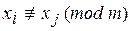3) " х_i : (х_i, m) = 1;

Пример: Пусть по модулю т = 10 имеется 10классоввычетов:

Z₁₀ 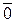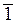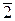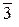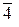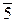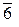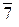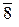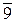= { , , , , , , , , , }– множество классоввычетов по модулю 10. Полная система вычетов по mod 10 будет, например, такая: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Множество классов вычетов, взаимно простых с модулем m=10: { 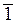, , 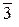, 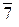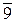}(j(10) = 4).

Приведённая система вычетов по модулю10 будет, например,

{1, 3, 7, 9}, или {11, 43, – 5, 17}, или { – 9, 13, – 5, 77} и т.д. (везде j(10) = 4 числа).

6.10. Практически: чтобы составить одну из возможных приведённых систем вычетов по mod m , нужно из полной системы вычетов по mod m выбрать те вычеты, которые взаимно простые с т. Таких чисел будет j(т).

6.11. Теорема 3.

Если {х₁, х₂,…, 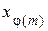} – приведённая система вычетов по модулю т и

(а, m) = 1, – то система чисел {ах₁, ах₂ , … , ах_j(т)} также образует

приведённую систему вычетов по модулю т .

6.12. Определение 6.

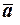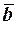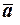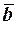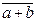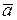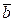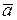Суммой ( Å ) классов вычетов и по модулю т называется класс вычетов , то есть класс вычетов, состоящий из чисел а + b, равных сумме любых двух вычетов, взятых по одному из каждого данного класса и : Å 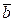= 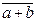, где "а Î 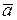, "b Î .

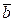6.13. Определение 7.

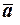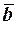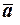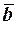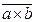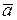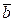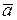Произведением ( Ä ) классов вычетов и по модулю т называется класс вычетов , то есть класс вычетов, состоящий из чисел а ´ b, равных произведению любых двух вычетов, взятых по одному из каждого данного класса и : Ä 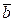= 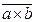, где "а Î 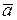, "b Î .

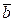Таким образом, в множестве классов вычетов по модулю т: Z_т = { 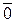, , 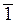,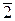…, 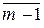} определены две алгебраические операции – "сложения" и "умножения".

6.14. Теорема 4.

Множество классов вычетов Z_т по модулю т является ассоциативно-коммутативным кольцом с единицей:

< Z_т , +, · > = < { 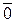, , 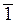,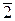…, 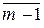}, +, · > – кольцо.

ТИПОВЫЕ ЗАДАЧИ

1. Составить по модулю т = 9:

1) полную систему наименьших положительных вычетов;

2) полную систему наименьших неотрицательных вычетов;

3) произвольную полную систему вычетов;

4) полную систему наименьших по абсолютной величине вычетов.

Ответ:1) {1, 2, 3, 4, 5, 6, 7, 8, 9}; 2) {0, 1, 2, 3, 4, 5, 6, 7, 8};

3) например, {10, – 7, 21, 49, – 4, 15, 25, – 1, 0}; 4) {– 4, – 3, – 2, – 1, 0, 1, 2, 3, 4}.

2. Составить приведённую систему вычетов по модулю т = 12.

Решение.

1) Составим полную систему наименьших положительных вычетов по модулю т = 12:

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} (всего т = 12 чисел).

2) Вычеркнем из этой системы числа, не взаимно простые с числом 12:

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.

3) Оставшиеся числа, взаимно простые с числом 12, образуют искомую приведённую систему вычетов по модулю т = 12 (всего j(т) = j(12) = 4 числа).

Ответ: {1, 5, 7, 11} – приведённая система вычетов по модулю т = 12.