ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

5. 1. Определение 1.

Целые числа a и b называются равноостаточными (или сравнимыми) по данному модулю т (т ÎN, т > 1), если при делении на число т они имеют равные остатки.

Число т называется модулем и обозначается mod m. Тогда запись вида

а º b (mod m) называется числовым сравнением (читается: число а сравнимо с числом b по модулю т).

В этой записи числа a и b сравнимы (равноостаточны) по модулю т .

Пример. Так как и число 8, и число 32 при делении на 6 имеют остаток r, равный 2, то эти числа сравнимы по mod 6, т. е. 8 º32(mod 6).

Аналогично 73 º– 27(mod 10) (остаток r = 3); 36 º12(mod 4) (остаток r = 0) и т.д.

5. 2. Лемма.

Для того, чтобы число a было сравнимо с числом b по модулю т, необходимо и достаточно, чтобы разность a – b делилась без остатка на т.

Пример. 73 º– 27(mod 10), так как 73 – (– 27) = 100, а 100 делится на 10. Обратно: 36 – 12 = 24, 24 делится на 4, значит, 36 º12(mod 4)

5. 3. Отметим, что если a = b, то а º b (mod m), где m – любое натуральное число, m > 1. Это означает, что равенство двух чисел есть частный случай их сравнимости. Обратное, вообще говоря, неверно.

5. 4. Свойства числовых сравнений, аналогичные свойствам числовых равенств.

1⁰ Рефлексивность: а º а (mod m).

2⁰ Симметричность: если а º b (mod m), – то b º а (mod m).

3⁰ Транзитивность: если а º b (mod m), b º с(mod m), – то а º с (mod m).

Следствие 1: Отношение сравнимости обладает свойством эквивалентности.

4⁰ Сравнения по одному и тому же модулю можно почленно складывать (вычитать):

если а º b (mod m), c º d (mod m), – то а ± c º b ± d (mod m).

Следствие 1: К обеим частям сравнения можно прибавить (вычесть) одно и то же целое число: если а º b (mod m), – то а ± к º b ± к (mod m) (кÎZ).

Следствие 2: Любое слагаемое можно перенести из одной части сравнения в другую с противоположным знаком: если а + с º b (mod m), – то а º– с + b (mod m).

5⁰ Сравнения по одному и тому же модулю можно почленно перемножать:

если а º b (mod m), c º d (mod m), – то а × c º b × d (mod m).

Следствие 1: Обе части сравнения можно умножить на одно и то же целое число к ¹ 0: если а º b (mod m), – то а × к º b × к (mod m).

Следствие 2: Обе части сравнения можно возвести в одну и ту же степень t Î N: если а º b (mod m), – то а ^t º b ^t (mod m).

Следствие 3: Если а º b (mod m) и f(x) = c_n xⁿ + c_{n – 1} x^{n – 1} + . . . + c₁ x + c₀, где c_i Î Z, – то f(a)º f(b) (mod m).

5. 5. Свойства числовых сравнений, зависящие от модуля (не аналогичные свойствам числовых равенств).

6⁰ К любой части сравнения (или к обеим частям) можно прибавить целое число, кратное модулю: если а º b (mod m), – то а ± kт º b ± tm (mod m), (k, t ÎZ).

7⁰ Обе части сравнения и модуль можно умножить на одно и то же число k Î N: если а º b (mod m), – то а × k º b × k (mod m × k).

8⁰ Вообще говоря, нельзя обе части сравнения делить на одно и то же целое число k ¹ 0.

Пример: 18º12(mod 6), однако 18 :3 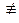12 :3(mod 6) (так как 6 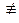4(mod 6).

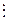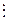9⁰ Но: обе части сравнения можно разделить на одно и то же целое число k ¹ 0, если оно взаимно простое с модулем. При этом частные будут сравнимы по тому же модулю: если а º b (mod m), где a k, b k и (k; m) = 1, – то а:к º b:к (mod m).

Пример: 35º21(mod 2), 35 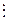7, 21 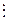7и (7; 2) = 1 Þ 35 :7º21 :7(mod 2), или 5º3(mod 2).

10⁰ Если обе части сравнения и модуль т делятся на одно и то же число k Î N, (k ¹ т) то частные от деления левой части и правой части сравнимы между собой по модулю, являющемуся частным от деления данного модуля на число k:

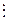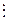если а º b (mod m), где a k, b k и т 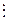k, – то a : k º b : k (mod т : k ).

Пример: 15º5(mod 10) Þ 15 :5º5 :5(mod 10 : 5), или 3º1(mod 2).

11⁰ Если а º b (mod m), где т 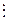п (п Î N, п >1) – то а º b (mod п).

12⁰ Если а º b (mod m₁), а º b (mod m₂) и т = НОК(m₁; m₂), – то а º b(mod m).

Пример: 49º1(mod 8), 49º1(mod 6) и НОК (8; 6) = 24 Þ 49º1(mod 24).

ТИПОВЫЕ ЗАДАЧИ

1. Установить, сравнимы ли числа а = 67 и b = – 23 по модулю 18.

Решение.

Составим разность а – b = 67 – (– 23) = 90. Так как а – b = 90 делится на 18, то по лемме 67 º– 23(mod18).

2. Установить, является истинными или ложными данные сравнения:

1) – 53 º– 38(mod5); 2) 3а + 2 º9 – 4а (mod7), "а Î Z.

Решение.

1) Составим разность ( – 53) – (– 38) = – 15. Так как –15 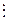5, то сравнение истинно.

2) Составим разность ( 3а + 2) – (9 – 4а) = 7а – 7 = 7(а – 1). Так как 7(а – 1) 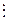7 при любом целом а, то сравнение истинно.

3. Доказать, что .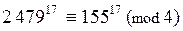

Решение.

1) 2 479 = 2 476 + 3 = 4×619 + 3 Þ 2 479 при делении на 4 даёт остаток r = 3,

155 = 152 + 3 = 4 × 38 + 3 Þ 155 при делении на 4 даёт остаток r = 3;

2) из шага 1) по определению 1 следует, что 2 479 º155(mod4);

3) по следствию 2 свойства 5⁰ числовых сравнений имеем: .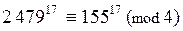

4. Упростить обе части сравнения 2238 а º4596 b (mod15), "а, b Î Z, а ¹ 0, b ¹ 0.

Решение.

1-й способ.

1) по свойству 6⁰ вычтем из каждой части сравнения числа, очевидно кратные модулю15:

2238 а – 1500 а º4596 b – 4500 b (mod15), то есть 738 а º96 b (mod15);

2) аналогично 738 а – 600 а º96 b – 90 b (mod15), то есть 138 а º6 b (mod15);

3) аналогично 138 а – 120 а º6 b (mod15), то есть 18 а º6 b (mod15);

4) аналогично 18 а – 15 а º6 b (mod15), то есть 3 а º6 b (mod15);

5) сократить обе части сравнения на 3 нельзя (!), так как (3; 15) ¹ 1 (свойство 8⁰).

Но: можно обе части сравнения и модуль разделить на 3 (свойство 10⁰), получим:

а º2 b (mod5).

2-й способ.

1) 2238 делим на15: 2238 = 15 ×149 +3. Значит, из левой части можно вычесть 15×149 а (свойство 6⁰): 2238 а – 15 ×149 а º4596 b (mod15), то есть 3 а º4596 b (mod15);

2) 4596 делим на15: 4596 = 15 ×306 +6. Значит, из правой части можно вычесть 15×306 b (свойство 6⁰): 3 а º4596 b – 15×306 b (mod15), то есть 3 а º6 b (mod15);

3) далее – см. 1-й способ, пункт 5). Ответ: а º2 b (mod5).