ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

ТЕОРИЯ ДЕЛИМОСТИ ЦЕЛЫХ ЧИСЕЛ

§ 1. ОТНОШЕНИЕ ДЕЛИМОСТИ В КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

1. ДЕЛЕНИЕ БЕЗ ОСТАТКА (НАЦЕЛО)

1. 1. Определение 1.

Пусть a, bÎZ, b ¹ 0. Говорят, что число a делится без остатка (нацело) на число b, если существует qÎZ такое, что. a = b × q (a – делимое, b – делитель, q – частное). Обозначение: a 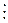b.

1. 2. Определение 2.

Два целых числа, отличающиеся друг от друга только множителями + 1 или – 1, называются ассоциированными.

Пример: + 5 и – 5, а и – а – ассоциированные числа.

1. 3. Основные свойства делимости (везде a, b, c – целые числа).

1⁰. Если a 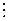b , b ¹ 0 – то a = b × q, причём q – единственное.

2⁰. Закон сокращения: из a × c = b × c (c ¹ 0) следует, что a = b.

3⁰. Если a ¹ 0, b ¹ 0 и если a b, – то .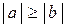

4⁰. Будем называть целое число a обратимым, если существует число a' ÎZ такое, что a × a' = 1. Во множестве Z обратимыми являются только числа + 1 и – 1.

5⁰. Делителями числа 1 являются только числа + 1 и – 1.

6⁰. Если a b и b a (a ¹ 0, b ¹ 0), – то b = ± a, то есть a и b – ассоциированные числа.

7⁰. Любое целое число делится на ± 1.

8⁰. Число 0 делится на любое целое число a , отличное от нуля.

9⁰. Отношение делимости рефлексивно: a (± a), где a ¹ 0.

10⁰. Отношение делимости транзитивно: если a b, b c, – то a c.

11⁰. Если a c и b c – то (a ± b) c. Обратно: если (a ± b) c и a c , – то b c.

12⁰. Если a b, b ¹ 0 и с – произвольное целое число , – то (a×c) b.

13⁰. Следствие из 11⁰ и 12⁰ :

Если a₁ c, a₂ c, ... , a_n c (c¹ 0) и " b₁ , b₂ , ... , b_n , – то

(a₁ b₁ + a₂ b₂ + ... + a_n b_n ) c.

14⁰. Если (a×c) (b×c), – то a b (c¹ 0).

2. ДЕЛЕНИЕ С ОСТАТКОМ

1. 4. Определение 3.

Пусть a, b Î Z, b ¹ 0. Разделить число a на число b с остатком – это значит: найти два целых числа q и r таких, что

a = b × q + r, где 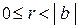(1)

(a– делимое, b – делитель, q – частное, r – остаток).

Примеры. 1) – 49 делим на 3: – 49 = 3×(– 17) + 2 (q = – 17, r = 2);

2) – 5 делим на – 7: – 5 = ( – 7) ×1 + 2 (q = 1, r = 2).

1. 5. Теорема 1.

Для любых a, b Î Z, b ¹ 0 существует единственная пара целых чисел q и r, удовлетворяющих условиям (1).

ТИПОВЫЕ ЗАДАЧИ

1. С помощью метода математической индукции доказать, что " п Î N: (2 × 4 ⁿ+ 1) 3.

Доказательство.

I. Проверим, что утверждение верно для п = 1: 2 × 4¹ + 1 = 9, 9 3 – истинно.

II. Допустим, что утверждение верно для некоторого натурального числа п = к, то есть допустим, что (2 × 4 ^к + 1) 3, или 2×4 ^к + 1 = 3 q, (qÎ Z), откуда 2 × 4 ^к = 3q – 1 (*)

III. Докажем, что утверждение верно для п = к +1, то есть докажем, что (2 × 4 ^к+1 + 1) 3.

В самом деле, 2 × 4 ^к+1 + 1 = 4 ×2 × 4 ^к + 1 = (по индуктивному допущению (*) )

= 4 ×(3 q – 1) + 1 = 12 q – 4 + 1 = 12 q – 3 = 3 × (4 q – 1) = 3 × q₁ (q₁Î Z) . Тогда по определению 1 (2 × 4 ^к+1 + 1) 3.

IV. На основании аксиомы математической индукции утверждаем, что (2 × 4 ⁿ+ 1) 3

при всех п Î N, ч. т. д.

2. Выполнить деление числа а на число в, если:

1) а = 74, в = – 32; 2) а = – 74, в = 32; 3) а = – 74, в = – 32; 4) а = 32, в = – 74.

Решение.

1)74 | – 32_ 64 – 2 = q 0 <10 = r < ½– 32½ Проверка: 74 = (–32)×(– 2) +10

2)– 74 | 32___ – 96 – 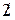–3 = q 0 < 22 = r < 32 Проверка: – 74 =32×(–3) + 22

3)– 74 | – 32___ – 96 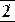3 = q 0 < 22 = r <½–32½ Проверка: – 74 =(– 32)×3 + 22

4)32 | – 74___ 0 0 = q 0 < 32 = r <½–74½ Проверка: 32 = – 74 ×0 + 32