ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

1. ОПРЕДЕЛЕНИЯ ПРОСТЫХ И СОСТАВНЫХ ЧИСЕЛ

3. 1. Определение 1.

Натуральное число р называется простым, если оно имеет два и только два различных делителя: 1 и само число р.

Например: 2, 3, 5, 7, 11, 13, 17, 19, . . . – простые числа.

3. 2. Определение 2.

Натуральное число п называется составным, если оно имеет по крайней мере три различных делителя.

Иными словами, существует d Î N , 1< d < п, такое, что п 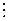d.

3. 3. Отметим, что п = 1 не является ни простым, ни составным числом.

3. 4. Лемма.

Всякое натуральное число п > 1 имеет по крайней мере один простой делитель р (то есть п 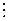р ).

3. 5. Теорема 1.

У всякого составного натурального числа п существует наименьший простой делитель р, удовлетворяющий условию: .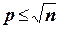

3. 6. Следствие 1.

Если ни одно из простых чисел, меньших 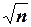, не является делителем натурального числа п, – то число п – простое .

3. 7. Теорема 2 – теорема Евклида .

Множество простых чисел бесконечно (иначе: не существует самого большого простого числа).

2. СВОЙСТВА ПРОСТЫХ ЧИСЕЛ

1⁰ Если число п – натуральное, р – простое, то либо п 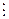р, либо (п; р) = 1 .

2⁰ Если р и q – простые числа и р 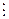q,– то р = q.

3⁰ Любые два неравные простые числа р и q (р ¹ q) – взаимно простые, т.е. (р; q) = 1.

4⁰ Если произведение нескольких целых чисел делится на простое число р, – то хотя бы один из множителей делится на р,

то есть если (а ×b) 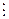р, – то либо a 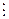р, либо b 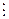р , либо и a 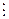р, и b 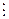р.

3. 8. Следствие 2. Если п² 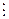р, – то п 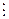р .

3. КАНОНИЧЕСКАЯ ФОРМА НАТУРАЛЬНОГО ЧИСЛА

(ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ ЦЕЛЫХ ЧИСЕЛ)

3. 9. Теорема 3.

Всякое натуральное число п > 1 можно однозначно (с точностью до порядка следования множителей) представить в виде произведения конечного числа простых чисел: п = р₁ × р₂ × …× р_t (все р_i – простые числа).

3. 10. Следствие 3. Объединив все равные простые числа, получим:

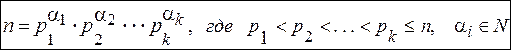(6)

3. 11. Определение 3.

Представление натурального числа п в виде (6) называется каноническим разложением (канонической формой) данного натурального числа.

Пример. Пусть п = 120. Тогда 120 = 2³ ×3¹ ×5¹ – каноническая форма числа 120.

3. 12. Основная теорема арифметики целых чисел устанавливает возможность представления любого числа п ÎN в виде (6).

ТИПОВЫЕ ЗАДАЧИ

1. Установить, является ли число п = 359 простым.

Решение.

1) Найдём 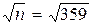= 18, … 2) Выпишем все простые числа, не превосходящие числа 18: 2, 3, 5, 7, 11, 13, 17. 3) Число п = 359 не делится ни на одно из этих чисел (проверьте!). Значит, п = 359 – простое число.

2. Даны числа а = 2520 и b = 825. 1) Представить эти числа в канонической форме; 2) найти d = НОД(a; b), m = НОК(a; b) и проверить справедливость равенства: d ×m = a ×b.

Решение.

1) Разложим числа а и b на простые множители и представим их в канонической форме.

2) Для нахождения d = НОД(a; b) из канонических разложений чисел а и b выпишем общие простые множители с наименьшими показателями степеней и перемножим их: d = 3 ×5 = 15.

3) Для нахождения т = НОК(a; b) из канонических разложений чисел а и b выпишем каждый простой множитель с наибольшим показателем степени и перемножим их: т = 2³ ×3² ×5² ×7¹ ×11¹ = 138 600.

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

(Примечание: в задачах этого параграфа a, b 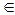Z, n 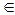N, p и q - простые числа).

74. Выпишите все простые числа, заключённые между 0 и 20.

75. Являются ли простыми данные числа:

а) n = 1; б) n = 2;в) n = 127; г) n = 109;

д) n = 177; е) n = 221; ж) n = 247; з) n = 281 ?

76. С помощью “решета Эратосфена” найдите все простые числа, заключённые между: а) 60 и 80; б) 100 и 120; в) 150 и 170; г) 190 и 210.

77. Известно, что простое число р делится без остатка на n. Какие значения может принимать n ?

78. Докажите, что если 0 < n < p, то НОД (n, p) = 1.

79. Докажите, что любое простое число р (р ³ 5) при делении на 6 даёт остаток 1 или 5.

95. Данные натуральные числа представьте в канонической форме:

а) 48; б) 72; в) 224; г) 131; д) 960; е) 1188; ж) 2535; з) 15400.

96. Установите, может ли число d быть делителем числа п и если может, то найдите частное п : d = q, где

а) n = 2³ × 5⁴ , d = 2² × 3 × 5³ ; б) n = 2³ × 3 × 5⁵ , d = 2² × 3 × 5³ ;

в) n = 3⁴ × 5² × 7³ , d = 3 × 5² × 7² ; г) n = 2 × 3⁵ × 7² , d = 2² × 3⁴ × 7.

97. Представьте данные числа a и b в канонической форме и найдите d = НОД (a, b) и m = НОК (a, b). Проверьте справедливость равенства: d × m = a × b.

а) a = 36, b = 24; б) a = 144, b = 192; в) a = 544, b = 2250;

г) a = 368, b = 552; д) a = 1694, b = 2695; е) a = 72765, b = 9075.

Глава 2. ЧИСЛОВЫЕ СРАВНЕНИЯ.

КЛАССЫ ВЫЧЕТОВ ПО ДАННОМУ МОДУЛЮ

§ 5. ЧИСЛОВЫЕ СРАВНЕНИЯ ПО ДАННОМУ МОДУЛЮ