ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
7. 1. Теорема 1.
Если аÎZ, тÎN, т >1 и (а; т) = 1 , – то в бесконечной последовательности степеней а1, а2, а3, ... , аs, … , аt, … найдутся хотя бы две степени с показателями s и t (s < t) такие, что 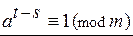 . (*)
. (*)
7. 2. Замечание. Обозначив t – s = k > 0, из (*) получим: 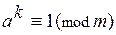 . Возводя обе части этого сравнения в степень nÎN , получим:
. Возводя обе части этого сравнения в степень nÎN , получим: 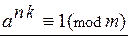 (**). Это означает, что существует бесконечное множество степеней числа a, удовлетворяющих сравнению (**). Но как найти эти показатели? Каков наименьший показатель, удовлетворяющий сравнению (**) ? На первый вопрос отвечает теорема Эйлера (1707 – 1783).
(**). Это означает, что существует бесконечное множество степеней числа a, удовлетворяющих сравнению (**). Но как найти эти показатели? Каков наименьший показатель, удовлетворяющий сравнению (**) ? На первый вопрос отвечает теорема Эйлера (1707 – 1783).
7. 3. Теорема Эйлера.
Если аÎZ, тÎN, т >1 и (а; т) = 1, – то 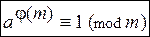 . (13)
. (13)
Пример. Пусть а = 2, т = 21, (а; т) = (2; 21) = 1. Тогда 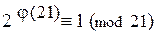 . Так как j (21) = 12, то 212 º 1(mod 21). В самом деле: 212 = 4096 и (4096 – 1)
. Так как j (21) = 12, то 212 º 1(mod 21). В самом деле: 212 = 4096 и (4096 – 1) 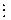 21. Тогда очевидно, что 224 º 1(mod 21), 236 º 1(mod 21) и так далее. Но является ли показатель степени 12 – наименьшим, удовлетворяющим сравнению 2n º 1(mod 21) ? Оказывается, нет. Наименьшим показателем будет п = 6: 26 º 1(mod 21), ибо 26 – 1 = 63, а 63
21. Тогда очевидно, что 224 º 1(mod 21), 236 º 1(mod 21) и так далее. Но является ли показатель степени 12 – наименьшим, удовлетворяющим сравнению 2n º 1(mod 21) ? Оказывается, нет. Наименьшим показателем будет п = 6: 26 º 1(mod 21), ибо 26 – 1 = 63, а 63 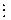 21. Заметим, что наименьший показатель следует искать только среди делителей числа j(т) (в данном примере – среди делителей числа j(21) = 12 ).
21. Заметим, что наименьший показатель следует искать только среди делителей числа j(т) (в данном примере – среди делителей числа j(21) = 12 ).
7. 4. Малая теорема Ферма (1601 – 1665).
Для любого простого числа р и любого числа аÎZ, не делящегося на р, имеет место сравнение 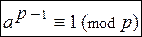 . (14)
. (14)
Пример. Пусть а = 3, р = 5, где 3 не 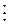 5. Тогда
5. Тогда 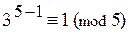 или
или 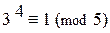 .
.
7. 5. Обобщёння теорема Ферма.
Для любого простого числа р и произвольного числа аÎZ имеет место сравнение 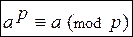 (15)
(15)
ТИПОВЫЕ ЗАДАЧИ
1. Докажите, что 38 73 º 3(mod 35).
Решение.
1) Так как (38; 35) = 1, то по теореме Эйлера 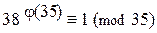 ; j(35) = 24, значит,
; j(35) = 24, значит,
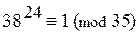 (1).
(1).
2) Из сравнения (1) по следствию 2 свойства 50 числовых сравнений имеем:
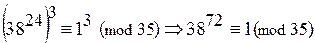 (2) .
(2) .
3) Из сравнения (2) по следствию 1 свойства 50 сравнений: 3872 ×38 º 1×38 (mod 35) Þ Þ38 73 º38 º 38–35 = 3(mod 35) Þ 38 73 º 3 (mod 35), что и требовалось доказать.
2. Дано: а = 4, т = 15. Найти наименьший показатель степени k, удовлетворяющий сравнению 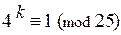 (*)
(*)
Решение.
1) Так как (a; m) = (4; 25) = 1, то по теореме Эйлера 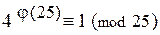 , j(25) = 20, поэтому
, j(25) = 20, поэтому 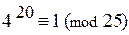 .
.
2) Является ли найденный показатель степени – число 20 – наименьшим натуральным числом, удовлетворяющим сравнению (*)? Если существует показатель степени, меньший 20, то он должен быть делителем числа 20. Значит, искомый наименьший показатель k надо искать среди множества чисел n = {1, 2, 4, 5, 10, 20}– делителей числа 20.
3) При п = 1: 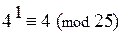 ;
;
при п = 2: 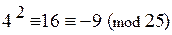 ;
;
при п = 3: (рассматривать не надо);
при п = 4: 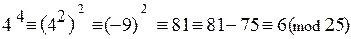 ;
;
при п = 5: 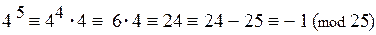 ;
;
при п = 6, 7, 8, 9: (рассматривать не надо);
при п = 10: 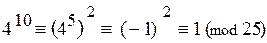 .
.
Итак, наименьшим показателем степени k, удовлетворяющим сравнению(*), является k= 10.
Ответ: 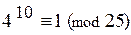 .
.
Дата добавления: 2017-12-05; просмотров: 507;
