ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

1. ЦЕЛЫЕ СИСТЕМАТИЧЕСКИЕ ЧИСЛА

8. 1. Определение 1.

Системой счисления называется всякий способ записи чисел. Знаки, с помощью которых записывают эти числа, называют цифрами.

8. 2. Определение 2.

Целым неотрицательным систематическим числом, записанным в t -ичной позиционной системе счисления, называется число n вида

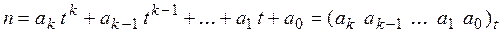, где a_i (i = 0,1, 2,…, k) – целые неотрицательные числа – цифры, причём 0 £ a_i £ t – 1, t – основание системы счисления, tÎN, t > 1.

Например, запись числа в 7-ричной системе имеет вид: (5603)₇ = 5 ×7³+ 6×7² + 0×7¹ + 3. Здесь a_i – это 5, 6, 0, 3 – цифры; все они удовлетворяют условию: 0 £ a_i £ 6. При t =10 говорят: число n записано в десятичной системе счисления, причём индекс t=10не пишут.

8. 3. Теорема 1.

Всякое целое неотрицательное число может быть представлено, причём единственным образом, в виде систематического числа по любому основанию t, где t Î N, t > 1.

Пример: (1 3 9) ₁₀ = (3 5 1) ₆ = (1 0 2 4) ₅ = …

8. 4. Отметим, что:

1) приписывание к систематическому числу нулей слева не изменяет этого числа:

(3 4)₅= (0 3 4)₅.

2) приписывание к систематическому числу s нулей справа равносильно умножению этого числа на t ^s: (3 4)₅ = 3×5¹ + 4; (3 4 0 0)₅ = 3×5³ + 4×5² + 0×5¹ + 0 = 5²×(3×5¹ + 4).

8. 5. Алгоритм перевода числа, записанного в t -ичной системе, в десятичную:

Пример: (287)₁₂= 2×12² + 8×12¹ +7×12⁰ = 2×144 + 8×12 + 7 = 288 + 96 +7 = (391)₁₀.

8. 6. Алгоритм перевода числа, записанного в десятичной системе, в t -ичную:

Пример: (3 9 1)₁₀ = (х)₁₂. Найти х.

Находим остатки от деления на основание системы t = 12: 1) данного числа 391 на 12, получим r₁= 7 ; 2) первого частного 32 на 12, получим r₂= 8 ; 3) второго частного 2 на 12, получим r₃= 2 ; Искомое число х составляется из остатков, записываемых последовательно, начиная с последнего: х = (2 8 7)₁₂ .	391 36 31 24
32 24
2
8 = r₂0 0
7 = r₁	2 = r₃

8. 7. Действия над систематическими числами

осуществляются с помощью таблиц сложения и умножения размером t ´ t. Например, при t = 2 таблицы имеют вид:	+	0 1		´	0 1
	0 1 1 10		0 0 0 1

2. СИСТЕМАТИЧЕСКИЕ ДРОБИ

8. 8. Определение 3.

Конечной t-ичной систематической дробью в системе счисления с основанием t называется число вида

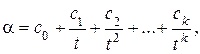где c₀ÎZ , с_i – цифры – целые неотрицательные числа, причём 0 £ с_i £ t – 1, t Î N, t > 1, k Î N .

Обозначение: a = (c₀, с₁с₂…с_k )_t. При t = 10 дробь называется десятичной.

8. 9. Следствие 1.

Всякая конечная систематическая дробь есть рациональное число, которое можно представить в виде 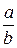, где а Î Z, b Î N.

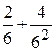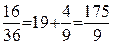Пример. a = (3 1, 2 4)₆ = 3×6 + 1 + =19 + – рациональное число. Обратное утверждение, вообще говоря, неверно. Например, дробь 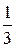нельзя преобразовать в конечную систематическую (десятичную) дробь.

8.10. Определение 4.

Бесконечной t-ичной положительной систематической дробью в системе счисления с основанием t называется число вида

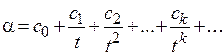, где с₀Î N, с_i (i =1, 2, …, к , …) – цифры – целые неотрицательные числа, причём 0 £ с_i £ t –1, tÎN, t >1, kÎN.

Обозначение: a = (с₀, с₁с₂… с_k …) _t. При t =10 дробь называется десятичной.

8.11. Определение 5.

Возможны три вида бесконечных систематических дробей:

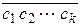
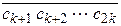
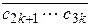
I a = (с₀, 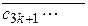)_t= = 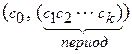_t , где 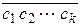= = 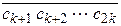= 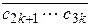… В этом случае число a называется бесконечной чисто периодической дробью, (с₁с₂… с_k) – периодом, k– количество цифр в периоде – длиной периода.

II a = .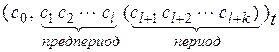

В этом случае число a называется бесконечной смешанной периодической дробью, – предпериодом, ( ) – периодом, k – количество цифр в периоде – длиной периода, l – количество цифр между целой частью и первым периодом – длиной предпериода.

III a = (с₀, с₁с₂… с_k … )_t . В этом случае число a называется бесконечной непериодической дробью.

ТИПОВЫЕ ЗАДАЧИ

1. Число (а)₅ = (2 1 4 3)₅, заданное в 5–ричной системе, перевести в 7-ричную систему, то есть найти х, если (2 1 4 3)₅ = (х)₇ .

Решение.

1) Преобразуем данное число (2 1 4 3)₅в число (у)₁₀, записанное в десятичной системе:

(2 1 4 3)₅ = 2×5³+1×5²+ 4×5+3 = = 2×125 +1×25 + 4×5 +3 =250 +25 + 20+3 = (2 9 8)₁₀. 2) Преобразуем полученное число (у)₁₀в семеричную систему (х)₇(см. справа): Ответ: (2 1 4 3)₅ = (6 0 4)₇.	298 28 18 14 4 = r₁
42 42
6
0 = r₂	0 0 6 = r₃

2. Выполните действия:

1) (7)₈ + (5)₈; 2) (7)₈ × (5)₈; 3) (3 6 4 2)₆ + (4 3 5 1)₆;

Times; (3 2) 5; 6) (3 0 1 4 1) 5 : (4 2 3) 5.

Решение.

1) (7)₈ + (5)₈= (7)₁₀ + (5)₁₀= (12)₁₀= 1×8 + 4 = (1 4)₈ ;

2) (7)₈ × (5)₈= (7)₁₀ × (5)₁₀= (35)₁₀= 4×8 + 3 = (4 3)₈ ;

3) (3 6 4 2)₆ ⁺(4 3 5 1)₆ (1 2 4 3 3)₆	Примечание:	4+5 = 9 = 1×6+3, 3 пишем, 1 переходит в следующий разряд, 6+3+1=10 =1×6+4, 4 пишем, 1 переходит в следующий разряд, 3+4+1= 8 = 1×6+2, 2 пишем, 1 переходит в следующий разряд.
4) (5 2 3 4)₇ ^–(2 3 5 1)₇ (2 5 5 3)₇	Примечание:	"занимаем" единицу высшего разряда, т. е. "1" = 1×7: (3 + 1×7 ) – 5 = 10 – 5 = 5, (1 + 1×7 ) – 3 = 8 – 3 = 5,
5) (4 2 3)₅ ^´( 3 2)₅ (1 4 0 1)₅ ⁺(2 3 2 4)_{5__} (3 0 1 4 1)₅	Примечание:	При умножении на 2 : 3 ×2 = 6 = 1×5 + 1, 1 пишем, 1 переходит в следующий разряд, 2 ×2 +1=5 = 1×5 +0, 0 пишем, 1 переходит в следующий разряд, 2 ×4 +1=9 = 1×5 +4, 4 пишем, 1 переходит в следующий разряд, При умножении на 3 : 3 ×3 = 9 = 1×5 + 4, 4 пишем, 1 переходит в следующий разряд, 3 ×2 +1=7 = 1×5 +2, 2 пишем, 1 переходит в следующий разряд, 3 ×4 +1=13=2×5 +3, 3 пишем, 2 переходит в следующий разряд.

6) (3 0 1 4 1)₅ | (4 2 3)₅

2 3 2 4 (3 2)₅

1 4 0 1

1 4 0 1 Ответ: 1) (1 4)₈; 2) (4 3)₈; 3) (1 2 4 3 3)₆; 4) (2 5 5 3)₇;

(0)₅ 5) (3 0 1 4 1)₅; 6) (3 2)₅.

<5 6 789 10 11 >

Дата добавления: 2017-12-05; просмотров: 1217;