УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

114. Запишите с помощью сравнения соотношение между данными числами, если известно, что: а) числа 17 и 62 при делении на 5 имеют одинаковые остатки;

б) число – 352 при делении на 31 даёт остаток, равный 20;

в) число 258 делится без остатка на 3.

115. Установите, сравнимы ли числа а и b по модулю т, если:

а) а = 18, b = 73, т = 5; б) а = – 34, b = 42, т = 11.

116. Установите, являются ли данные сравнения истинными или ложными:

а) 35 º – 75 (mod 10); б) 81 º – 4 (mod 3); в) 18 º 33 (mod 15);

г) 2³ º 1 (mod 4); д) 546 º 0 (mod 13); е) 5435 º 77 (mod 5);

ж) 3m º 5m (mod m); з) 8m – 5 º 11m –5 (mod m); и) 3m º1 (mod m) (m>1);

к) (m – 1)² º 1 (mod m); л) 30 × 19 º 81× 17 (mod 6); м) 5¹⁹⁹⁸ º 1999 (mod 5).

117. Докажите: если a 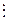т, где а Î Z, т Î N, т >1, – то а º0(mod m) и обратно.

118. Запишите с помощью сравнения множество нечётных чисел п = 2к + 1.

119. Запишите множество значений переменной х, удовлетворяющих сравнению:

а) х º 5 (mod 7); б) х º 0 (mod 17); в) 3 х º 1 (mod 2).

120. Приведите примеры целых чисел, сравнимых с числом 7 по модулю 9.

121. Приведите примеры целых чисел, сравнимых по модулю 11.

122. Упростите данное сравнение, сопровождая каждое преобразование ссылкой на соответствующее свойство числовых сравнений:

а) 30 – 40 m + 7 n º 5 m – 36 – 20 n (mod 12); б) 27a +17+ b º19 b – 31 (mod 48).

123. Докажите: если a º b (mod m) и m 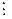n, то a º b (mod n).

124. Докажите: а) 1² + 3² + 5² + 7² º 4 (mod 10); б) 1⁴ + 2⁴+ 3⁴ + 4⁴ + 5⁴ º – 1 (mod 10).

125. Запишите с помощью числового сравнения множество всех чисел, оканчивающихся а) в десятичной системе счисления - на 3; б) в 7 -ричной системе счисления - на 5.

126. Пользуясь свойствами числовых сравнений, найдите остаток от деления:

а) числа 38² на 6; б) числа 2002² на 5; в) числа 57³ на 9; г) числа 2375⁴ на 8.

127. Найдите остаток от деления: а) 12 ¹⁰⁰ на 15; б) числа (23 642 540) ⁴ на 7;

в) 6 ¹⁰⁰⁰ на 8; г) числа (195 743 264) ¹⁴ на 6. .

128. Докажите, что: а) 3 ^4п – 1 (где п Î N) делится без остатка на 80;

б) 2 ^5п + 1 (где п - нечётное число) делится без остатка на 33;

в) 1 + 3 ^{3п + 1} + 9 ^{3п + 1} (где п Î N) делится без остатка на 13.

129. Докажите: если aºb (mod m₁) и aºb (mod m₂), то aºb (mod т), где т = НОК(m₁, m₂)

§ 6. КЛАССЫ ВЫЧЕТОВ ПО МОДУЛЮ т .