ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ (НОД) НЕСКОЛЬКИХ ЦЕЛЫХ ЧИСЕЛ
2. 1. Определение 1.
Целое число d называется общим делителем данных целых чисел а1, а2 , …, ап, если каждое из этих чисел делится на d без остатка, то есть: а1 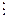 d, а2
d, а2 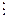 d, …, ап
d, …, ап 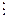 d.
d.
2. 2. Определение 2.
Целое число d > 0 называется наибольшим общим делителем данных целых чисел а1, а2 , …, ап, если:
а) каждое из этих чисел делится на d (то есть d – их общий делитель); б) d делится на любой другой общий делитель d этих чисел.
Обозначение: d = НОД (а1, а2 , …, ап) или, короче, d = (а1, а2 , …, ап).
Пример.
Пусть а = 56, b = 32. Тогда d = ОД(а; b) = ОД(56; 32) ={± 1; ± 2; ± 4; ± 8}.
d = НОД(а; b) = НОД(56; 32) = 8 (выполняются оба условия а) и б) – проверьте!).
2. 3. Теорема 1.
Для любых а1, а2 , …, ап Î Z, их наибольший общий делитель
d = НОД (а1, а2 , …, ап) = НОД ( НОД (а1, а2 , …, ап – 1), ап) .
Пример. НОД (56; 32; 20) = НОД ( НОД (56; 32); 20) = НОД (8; 20) = 4.
2. 4. Алгоритм Евклида.
I. ЛЕММЫ
I. Если а 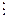 b, – то НОД (а; b) =½b½ (а, b Î Z, b ¹ 0) .
b, – то НОД (а; b) =½b½ (а, b Î Z, b ¹ 0) .
II. НОД (0; b) =½b½ (b ¹ 0) .
III. Если a = b × q + r, где 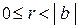 , а, b, q, r Î Z, – то НОД (а; b) = НОД (b; r).
, а, b, q, r Î Z, – то НОД (а; b) = НОД (b; r).
II. А ЛГОРИТМ ЕВКЛИДА ДЛЯ НАХОЖДЕНИЯ НОД
Пусть а, b Î Z, b ¹ 0. Выполним последовательно деление:
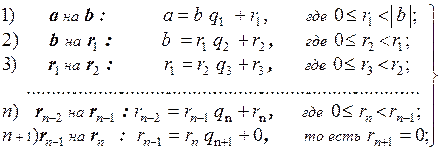 ½b½>r1> r2>…>rn> rn+1 = 0
½b½>r1> r2>…>rn> rn+1 = 0
Тогда НОД (а; b) = r п ¹ 0. (1)
Наибольший общий делитель равен последнему отличному от нуля остатку.
2. 5. Линейное представление НОД нескольких чисел.
1) Теорема 2.
Если НОД(а, b) = d, где а, b Î Z, – то существуют числа с1, с2 Î Z такие, что а× с1 + b× с2 = d (2)
Это равенство называется линейным представлением НОД , то есть с помощью равенства (2) d линейно выражается через данные числа а и b.
Пример. Пусть а = 6, b = 8. Имеем: d = НОД (6; 8) = 2. Тогда
6 × (– 1) + 8 × 1 = 2 = d, или 6 × 3 + 8 ×(– 2) = 2 = d, или 6 × 11 + 8 × (– 8) = 2 = d и т.д.
2) Обобщение теоремы 2.
Если НОД(а1, а2 , …, ап) = d, – то существуют числа с1, с2 , …, сп Î Z такие, что а1× с1 + а2× с2 + … + ап× сп = d (2а)
2. 6. Свойство НОД.
Общий множитель чисел а и b можно вынести за знак их НОД:
НОД (ka; kb) = k × НОД (a; b) , ( k Î N) (3)
Пример.
НОД (144; 120) = 12 ×НОД (12; 10) = 12 ×2 × НОД (6; 5) = 12 × 2 ×1 = 24.
2. ВЗАИМНО ПРОСТЫЕ ЧИСЛА
2. 7. Определение 3.
Целые числа а1, а2 , …, ап называется взаимно простыми, если их наибольший общий делитель равен единице.
Пример.
НОД (8; 9; 45) = 1, значит, числа 8, 9, 45 – взаимно простые.
2. 8. Свойства взаимно простых чисел.
10 Для того, чтобы числа а1, а2 , …, ап были взаимно простыми, необходимо и достаточно, чтобы существовали числа с1, с2 , …, сп Î Z такие, что а1× с1 + а2× с2 + … + ап× сп = 1
20 Если (а×b) 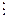 c и (b; c) = 1, – то a
c и (b; c) = 1, – то a 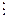 c .
c .
30 Если (a; c) = 1, (b; c) = 1, – то (a×b; c) = 1.
40 Если (а; b) = d ( и учитывая, что a 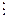 d, b
d, b 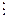 d), – то (a : d; b : d) = 1.
d), – то (a : d; b : d) = 1.
3. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ (НОК) НЕСКОЛЬКИХ ЦЕЛЫХ ЧИСЕЛ
2. 9. Определение 4.
Целое число М называется общим кратным данных целых чисел а1, а2 , …, ап, если число М делится без остатка на каждое из этих чисел, то есть: М 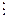 а1, М
а1, М 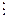 а2, …, М
а2, …, М 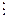 ап.
ап.
2. 10. Определение 2.
Целое число т > 0 называется наименьшим общим кратным данных целых чисел а1, а2 , …, ап, если:
а) число т делится на каждое из чисел а1, а2 , …, ап (то есть т является их общим кратным);
б) любое другое общее кратное М этих чисел делится на т..
Обозначение: т = НОК (а1, а2 , …, ап) или, короче, т = [а1, а2 , …, ап].
Пример.
Пусть а = 6, b = 8. Тогда M = OK (а; b) = OK (6; 8) = {± 24; ± 48; ± 72; ± 96; …}.
m = [а; b] = HOK(6; 8) = [6; 8] = 24 (выполняются оба условия а) и б) – проверьте!).
2. 11. Теорема 3.
Для любых а1, а2 , …, ап Î Z их наименьшее общее кратное
т = НОК (а1, а2 , …, ап) = НОК ( НОК (а1, а2 , …, ап – 1), ап) .
Пример. НОК (6; 8; 10) = НОК ( НОК (6; 8); 10) = НОК (24; 10) = 120.
2. 12. Свойства НОК.
10 Если (а; b) = 1, a; b Î N, – то НОК (a; b) = a × b.
20 Общий множитель чисел а и b можно вынести за знак их НОK:
НОК (ka; kb) = k × НОК (a; b) (k Î N). (4)
30 Если m = НОК (a; b) ( и учитывая, что m 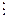 a, m
a, m 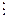 b), – то (m : a; m : b) = 1.
b), – то (m : a; m : b) = 1.
4. СВЯЗЬ НОД и НОК ДВУХ НАТУРАЛЬНЫХ ЧИСЕЛ
2. 13. Теорема 4.
Для любых а, b Î N:НОД (а; b) × НОК (а; b) = a × b ( 5)
2. 14. Следствие.
Для любых а, b Î N: 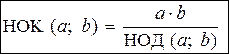 (5а)
(5а)
ТИПОВЫЕ ЗАДАЧИ
1. С помощью алгоритма Евклида найти: а) НОД (56; 32); б) НОД (56; – 32).
| Решение. | a) 56 |_32_ 32 1 = q1 32 |_24_ = r1 24_ 1 = q2 24 |_8_ = r2 = d 24_ 3 = q2 0 = r3 | б) 56 | – 32_ 32 –1 = q1 – 32 | 24 = r1 – 48 – 2 = q2 24 |16 = r2 16 1 = q3 16 | 8_ = r3 = d 16 2 = q4 0 = r4 |
Ответ: а) НОД (56; 32) = r2 = 8; б) НОД (56; – 32) = r3 = 8.
2. Составить линейное представление наибольшего общего делителя чисел а =56 и b = – 32 через эти числа.
Решение.
1) С помощью алгоритма Евклида найдём d = НОД (56; – 32) (см. пример 1 б) ).
Заметим, что здесь r1 = 24, r2 = 16, r3 = 8, r4 = 0, q1 = –1, q2 = – 2, q3 = 1. При этом d = НОД (56; – 32) = r3 = 8.
2) Подберём коэффициенты с1 и с2 Î Z так, чтобы по (2) а× с1 + b× с2 = d.
Согласно алгоритму Евклида имеем:
a = b × q1+ r1 , или a = b × (– 1) + r1 , откуда r1 = a + b;
b = r1× q2+ r2 , или b = r1× (– 2) + r2 , откуда r2 = b + 2 r1= b + 2a + 2b = 2a + 3b;
r1= r2× q3+ r3 , или r1= r2 × 1 + r3 , откуда r3 = r1– r2= (a+b)–(2a+3b) = – a – 2b.
3) Итак, d = r3 = – a – 2b. Проверка: – a – 2b = – 56 – 2×( – 32) = 64 – 56 = 8 = d.
Ответ: d = – a – 2b, то есть с1 = – 1 и с2 = – 2.
3. Найти наименьшее общее кратное чисел а =56 и b = 32.
Решение.
1-й способ. По формуле ( 5 ) : НОК (56; 32) = 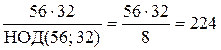 .
.
2-й способ. По формуле ( 4 ): НОК (56; 32) = 8 × НОК (7; 4) = 8×7×4 = 224 (учитывая,
что 7 и 4 – взаимно простые).
Ответ: НОК (56; 32) = т = 224.
4. Сократить дробь: 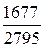 .
.
Решение.
1) С помощью алгоритма Евклида найдём d = НОД (1677; 2795) = 559. Это означает, что числитель и знаменатель делятся на 559, то есть дробь сократима на 559.
2) Поэтому 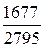 =
= 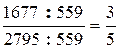 . Ответ:
. Ответ: 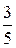 .
.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
21. Пусть НОД (а, b) = d, a > b. Может ли быть d = 1; d = –3; d = 0 ?
22. Пусть НОД (а, b) = d, a > b > 0. Может ли быть d > b; d = b; d < b ?
23. Пусть НОД (а, b) = d, a < b. Может ли быть d < a; d = a; d > a ?
24. Пусть a ÎN. Чему равен НОД (а, 1) ? НОД (а, 0) ? НОД (– а, 1) ? НОД (– а, – 1) ?
25. С помощью алгоритма Евклида найдите наибольший общий делитель данных целых чисел:
а) 336 и 640; б) 288 и 300; в) 85 и 76; г) 144 и 160; д) 189 и 21;
е) 851 и 690; ж) 306 и 340; з) 75 и 300; и) 190 и 266; к) – 92 и 130;
л) – 70 и 56; м) –600 и 756; н) – 48 и – 72; о) – 39 и – 35; п) – 24 и 60.
26. Докажите формулу (3): НОД (kа, kb) = k × НОД (а, b) (kÎN) .
27. Найдите наибольший общий делитель данных чисел с помощью формулы (3):
а) 48 и 72; б) 144 и 90; в) 120 и 270; г) 35 и 33.
28. Найдите наибольший общий делитель чисел:
а) 126, 420 и 525; б) 120, 300 и 330; в) 270, 288 и 900;
г) 56, 72, 48 и 100; д) 126, 90, 84 и 54. е) 87, 93 и 79.
29. Найдите наибольший общий делитель числителя и знаменателя и сократите дроби:
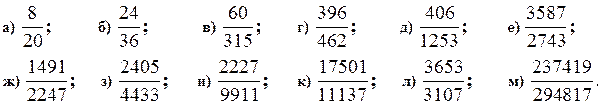
В примерах 33 – 46 осуществите линейное представление наибольшего общего делителя d данных чисел a и b через эти числа (то есть подберите коэффициенты c1и c2 так, чтобы выполнялось равенство: d = a c1 + b c2 ).
33. a = 28, b = 20. 34. a = 18, b = 14. 35. a = 88, b = 14. 36. a = 27, b = –21.
37. a = –56, b = 18. 38. a = 90, b = 35. 39. a = –27, b = 21. 40. a = –36, b = 63.
41. a = 1232, b =1672. 42. a = 77, b = 8. 43. a = 174, b = –26. 44. a = –136, b =25.
45. a = 88, b = – 14. 46. a = – 86, b = 56.
В примерах 47 – 48 подберите коэффициенты k1, k2 и k3 так, чтобы выполнялось равенство: НОД (а, b, с) = d = a k1 + b k2 + с k3 .
47. а = 50, b = 46, с = 34. 48. а = 174, b = 33, с = – 26.
49. Определите, являются ли данные три числа взаимно простыми, либо попарно взаимно простыми, либо одновременно и теми, и другими:
а) а = 16, b = 27, с = 25; б) а = 8, b = 15, с = 12;
в) а = 6, b = 1; с = 14; г) а = 10, b = 27, с = 77.
50. Дано: (а, b) = 1, (b, c) = 1. Следует ли отсюда, что (а, c) = 1 ?
51. Найдите наименьшее общее кратное данных чисел:
а) 48 и 72; б) 36 и 54; в) 180 и 350; г) 264 и 165; д) 600 и 756;
е) 273 и 455; ж) 206 и 291; з) 78, 39 и 65; и) 270, 288 и 900; к)72, 120, 180 и 240.
52. Найдите наименьший общий знаменатель данных дробей:
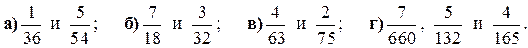
53. Докажите формулу (4): НОК (kа, kb) = k × НОК (а, b) (kÎN).
54. Найдите наименьшее общее кратное данных чисел с помощью формулы (4):
а) 24 и 96; б) 75 и 100; в) 95 и 55; г) 84 и 210.
§ 3. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА.
Дата добавления: 2017-12-05; просмотров: 1797;
