Рекурсивные алгоритмы. Алгоритм RLS.

Алгоритм (3.2) является вычислительно сложным из-за большого количества операций комплексного перемножения при формировании оценок корреляционной матрицы 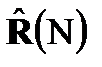и вектора корреляции 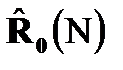и последующего обращения матрицы с ее перемножением на вектор. Эти операции надо повторять на каждом шаге.

Сократить вычислительные затраты можно, если на каждом шаге не заново оценивать матрицу, а лишь уточнять ее значение с использованием вновь полученной дискретной выборки входных сигналов. Это дает возможность организовать вычисления рекурсивно. Соответствующий алгоритм называется рекурсивным методом наименьших квадратов (Recursive Least Square, RLS).

Итерационный способ обращения матрицы основан на ее представлении в виде:

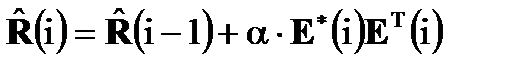, (4.1)

где 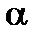- вес текущей оценки матрицы.

В этом случае после выполнения математических преобразований результирующая рекурсивная оценка обратной матрицы описывается выражением:

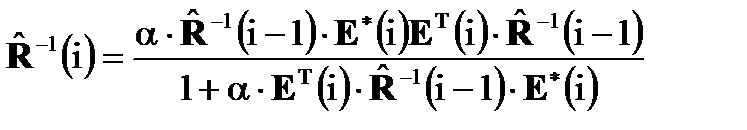. (4.2)

Соответственно, алгоритм рекуррентного формирования весового вектора примет вид:

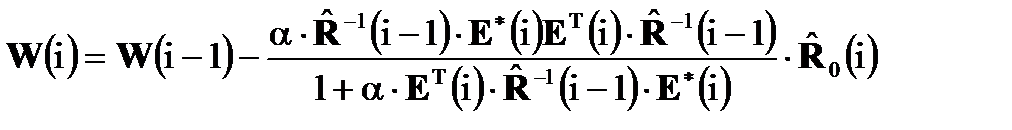. (4.3)

Главным достоинством алгоритма RLS является его быстрая сходимость. Однако это достигается более высокой вычислительной сложностью по сравнению с алгоритмом LMS: на каждом такте требуется (2.5N²+4N) операций «умножение-сложение».