Эффекты квантования коэффициентов цифрового фильтра

При реализации цифровой системы значения ее коэффициентов квантуются из-за представления ограниченным количеством разрядов. Изменение коэффициентов приводит к изменению частотных характеристик системы. Наибольшие искажения происходят, когда АЧХ фильтра имеет крутые скаты в переходных зонах. Для рекурсивных фильтров возможна даже потеря устойчивости.

Существуют два подхода к анализу эффектов квантования коэффициентов фильтров: статистический и прямой оптимизации. В первом случае оцениваются среднеквадратические отклонения частотной характеристики от исходной. Во втором случае производится прямая оптимизация квантованных коэффициентов с учетом реальной сетки возможных значений.

Например, передаточная функция цифрового резонатора, полученная по аналоговому прототипу резонансного контура, имеет следующий вид:

, (4.1)

где ;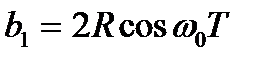

;

;

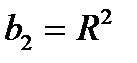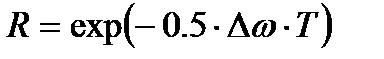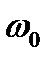- резонансная частота аналогового прототипа;

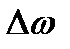- полоса пропускания аналогового прототипа.

Коэффициент 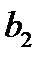влияет только на полосу пропускания цифрового фильтра:

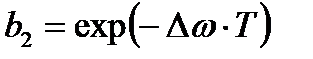. (4.2)

Если в результате округления значение коэффициента 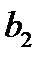меняется:

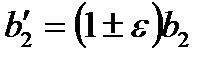, (4.3)

то будет меняться и полоса пропускания цифрового фильтра:

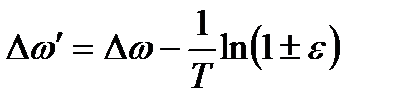. (4.4)

Резонансная частота зависит от обоих коэффициентов цифрового фильтра:

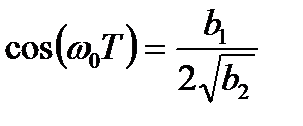. (4.5)

Соответственно, при ошибках округления можно записать:

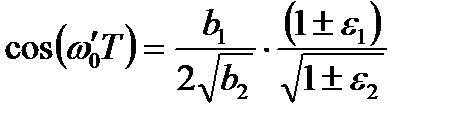. (4.6)

После преобразований получим:

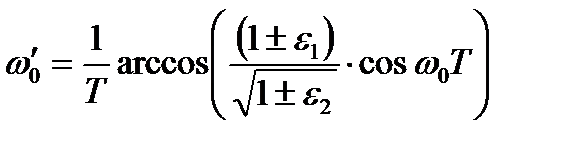. (4.7)

Предельные циклы

Ранее при рассмотрении эффектов квантования в перемножителях были сделаны допущения о независимости шумов квантования в отдельные моменты времени и не учитывалось переполнение регистров сумматоров. В результате нарушения этих предположений возникают специфические эффекты предельных циклов.

Существуют два типа предельных циклов:

- предельные циклы низкого уровня;

- предельные циклы высокого уровня.

Предельными циклами низкого уровня называются незатухающие колебания, возникающие в рекурсивных фильтрах при ненулевых начальных условиях и при отсутствии воздействия. Появление этих колебаний обусловлено квантованием сигналов на выходах умножителей. В отличие от импульсной характеристики аналоговых фильтров протяженность дискретных импульсных характеристик рекурсивных фильтров ограничена во времени. По мере уменьшения отсчетов импульсной характеристики они достигают интервала квантования по уровню и исчезают. Однако при неудачно выбранных значениях коэффициентов цифрового фильтра или их разрядности отсчеты дискретной импульсной характеристики, достигнув значения , сохраняют его до бесконечности. Такое явление и называется возникновением предельного цикла малого уровня.

В качестве примера рассмотрим рекурсивный фильтр 1-ого порядка:

.

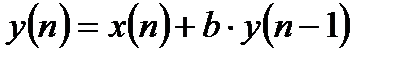Если использовать десятичную систему исчисления и учитывать только один знак после запятой, то для коэффициента 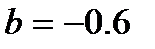получим импульсную характеристику c предельным циклом малого уровня.

Рисунок 5.2 – дискретная импульсная характеристика рекурсивного цифрового фильтра 1-ого порядка с предельным циклом

При обработке речевых сигналов предельный цикл проявляется в виде помехового свиста в паузах между речевыми сообщениями.

Исключают эффект предельного цикла следующими способами:

- увеличением разрядности коэффициентов цифрового фильтра;

- изменением значений коэффициентов за счет варьирования частоты дискретизации;

- изменением значений коэффициентов за счет изменения структуры цифрового фильтра.

Основы цифровой обработки сигналов: учебное пособие / Ю.А. Брюханов, А.А. Приоров, В.И. Джиган, В.В. Хрящев; Яросл. гос. ун-т им. П.Г. Демидова. - Ярославль: ЯрГУ, 2013. – 344 с. (с.162)

Предельные циклы высокого уровнясвязаны с переполнением регистров сумматоров. Если используется представление чисел в дополнительном коде, из-за цикличности арифметики выход соответствующего узла цепи перескакивает с максимально положительного значения диапазона представления

на минимальное отрицательное или наоборот. Это вызывает большие пульсации в выходном сигнале цепи. Для борьбы с этим явлением можно использовать два способа. Первый заключается в нормализации, чтобы избежать возможности переполнения. Второй состоит в использовании арифметики с насыщением, когда при переполнении в результат подставляют максимальное по абсолютному значению число,

имеющее тот же знак, что и сумма (произведение).

Глинченко А.С. Цифровая обработка сигналов: в 2 ч. Ч.1. Красноярск: Изд-во КГТУ. 2001. 199 с. (п. 4.3, 4.4: выбор масштабных множителей, исключающих переполнение сумматоров)

Основы цифровой обработки сигналов: учебное пособие / Ю.А. Брюханов, А.А. Приоров, В.И. Джиган, В.В. Хрящев; Яросл. гос. ун-т им. П.Г. Демидова. - Ярославль: ЯрГУ, 2013. – 344 с. (с. 159, 164)