Постановка задачи. Градиентные алгоритмы аналоговой адаптации

Пусть используется критерий оптимальности адаптивного фильтра в виде минимума выходной мощности. В качестве ограничения используем равенство единице одного из весовых коэффициентов адаптивного фильтра. В этом случае структура адаптивного пространственного фильтра примет вид, приведенный на рисунке 1.1.

Необходимо получить алгоритмы формирования дискретных цифровых значений весовых коэффициентов, минимизирующих выбранный критерий оптимальности.

Для этого сформируем аналоговый прототип формирования весовых коэффициентов и после этого осуществим переход к дискретным цифровым алгоритмам. В качестве аналогового прототипа формирования весовых коэффициентов воспользуемся градиентным алгоритмом.

Градиентный алгоритм заключается в интегрировании сигнала ошибки, в качестве которого выступает градиент используемого критерия качества по формируемым весовым коэффициентам:

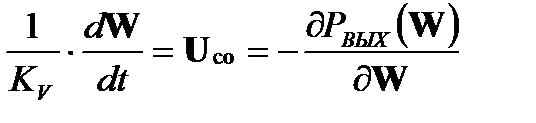, (1.1)

где 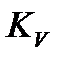- коэффициент преобразования интегратора.

Знак минус в алгоритме обеспечивает соблюдение условия устойчивости и возвращение весовых коэффициентов в оптимальное значение после некоторого отклонения от него.

Рисунок 1.1 – структура адаптивного пространственного фильтра, реализующего критерий минимума выходной мощности с ограничением значения одного из весовых коэффициентов

С учетом выбора критерия качества в виде минимума выходной мощности помехи вектор сигналов ошибок запишется следующим образом:

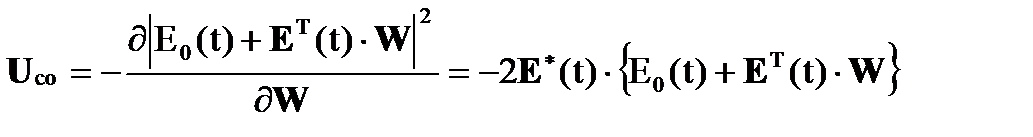. (1.2)

Система дифференциальных уравнений, описывающая работу аналогового адаптивного фильтра, реализующего градиентный способ формирования весовых коэффициентов для критерий минимума выходной мощности, имеет следующий вид:

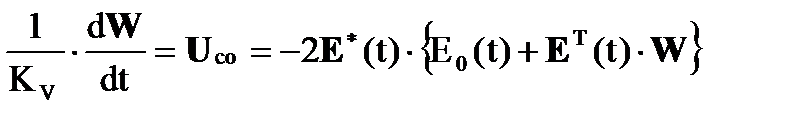. (1.3)

Структурная схема полученного аналогового адаптивного фильтра приведена на рисунке 1.2.

Рисунок 1.2 - Структурная схема аналогового адаптивного фильтра с градиентным формированием весовых коэффициентов