Теорема о прямом угле

Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 45).

Дано:∠ABC = 90º; AB∥π₁.

Доказать, что В₁С₁⊥A₁B₁.

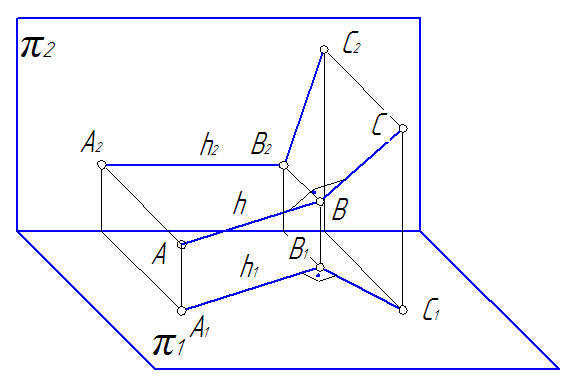
Рис. 45

Доказательство: если AB∥ π₁, то A₁B₁∥AB, но ВВ₁⊥ π₁ ⇒ ВВ₁⊥A₁B₁ значит AB⊥ ВВ₁ и AB⊥ плоскости (ВВ₁ ∩ ВС), тогда и A₁B₁⊥CВВ₁C₁. Следовательно, C₁A₁⊥A₁B₁.

На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на π₁в виде взаимно перпендикулярных прямых (рис. 46а), если одна из них горизонталь, на π₂ – если одна из них фронталь (рис. 46б).

а) б) в)

Рис. 46

Условие перпендикулярности скрещивающихся прямых (рис. 46в) сводятся к условиям перпендикулярности пересекающихся прямых, проведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.

Контрольные вопросы

1. Что такое следы прямой и как они определяются?

2. Как находится натуральная величина длинны отрезка и угол наклона этого отрезка к плоскости проекций?

3. Какую проекцию отрезка необходимо принять за катет чтобы определить угол наклона отрезка к фронтальной плоскости проекций?

4. Характерные признаки определения взаимного расположения прямых по эпюру Монжа (пересечение, параллельность, скрещивание)?

5. Сформулируйте теорему о проецировании прямого угла пересекающихся прямых.

6. Сформулируйте условия о проецировании прямого угла двух скрещивающихся прямых.