Главные прямые плоскости

Основными главными линиями плоскости являются: горизонтали плоскости; фронтали плоскости; профильные прямые плоскости; линии наибольшего ската; линии наибольшего наклона; линия наибольшего наклона к профильной плоскости. В данной лекции профильные прямые плоскости и линии наибольшего наклона к профильной плоскости проекций не рассматриваются.

Горизонталь плоскости. Горизонталь плоскости – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости проекций. На рис. 58 показана горизонталь h плоскости α.

Алгоритм построения горизонтали (рис. 59).

1. Горизонталь плоскости как прямая, параллельная горизонтальной плоскости проекций, имеет фронтальную проекцию h₂, параллельную оси 0Х. Поэтому вначале на фронтальной проекции заданной плоскости строит­ся характерный признак горизонтали. На рис. 59 h₂(С₂1₂)∥0X.

2. По принадлежности прямой плоскости (алгоритм принадлежности прямой плоскости) достраивается недостающая проекция горизонтали плоскости h₁.

Рис. 58 Рис. 59

Следует отметить, что все горизонтали плоскости параллельны между собой и параллельны горизонтальному следу плоскости.

Фронталь плоскости. Фронталь плоскости – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости проекций. На рис. 60 показана фронталь f плоскости α.

Алгоритм построения фронтали (рис. 61).

1. Фронталь плоскости как прямая, параллельная фронтальной плос­ко­сти проекций, имеет горизонтальную проекцию f₁, параллельную оси 0Х. Поэтому вначале на горизонтальной проекции заданной плоскости строится характерный признак фронтали. На рис. 61 f₁(A₁1₁)∥0X.

2. По принадлежности прямой плоскости (алгоритм принадлежности прямой плоскости) достраивается недостающая проекция горизонтали плоскости f₂.

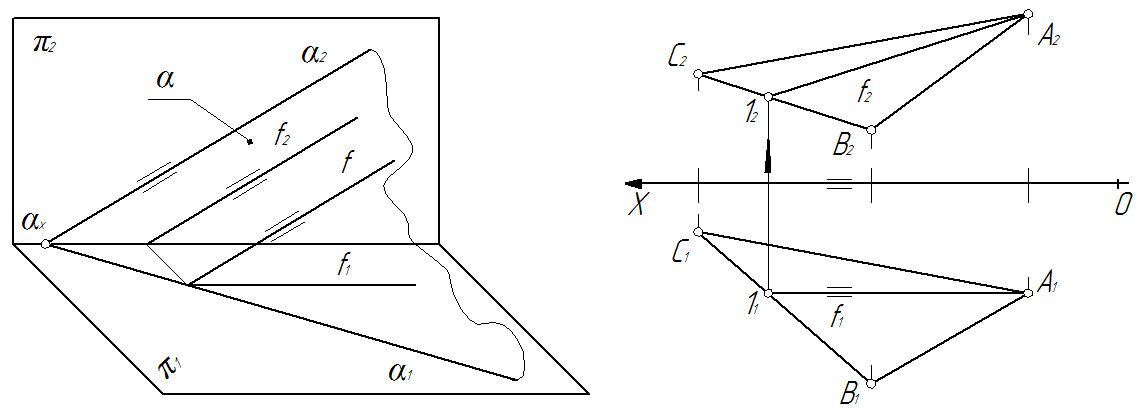
Рис. 60 Рис. 61

Линия наибольшего ската. Линия наибольшего ската – прямая, которая лежит в этой плоскости и перпендикулярная горизонталям этой плоскости. Угол α (рис. 62) между линией наибольшего ската и ее горизонтальной проекцией равен углу наклона плоскости к горизонтальной плоскости проекций. Поэтому линия наибольшего ската характеризует угол наклона плоскости к горизонтальной плоскости проекций.

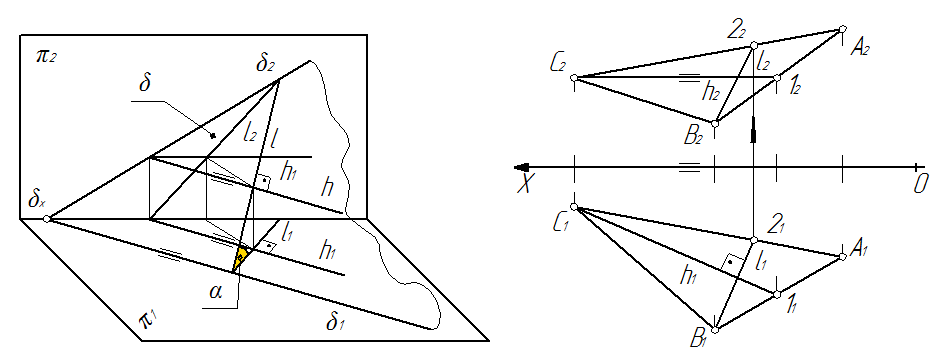
Рис. 62 Рис. 63

Алгоритм построения линии наибольшего ската (рис. 63).

1. В заданной плоскости проводится горизонталь h.

2. Используя теорему о прямом угле, на первой проекции плоскости, строится проекция линии наибольшего ската l₁(В₁2₁)^h₁(C₁1₁).

3. По принадлежности прямой плоскости достраивается недостающая проекция l₂ линии наибольшего ската.

Следует отменить, что все линии наибольшего ската параллельны между собой и перпендикулярны горизонтальному следу плоскости.

Линия наибольшего наклона. Линия наибольшего наклона – прямая, которая лежит в этой плоскости и перпендикулярная фронталям этой плоскости. Угол β(рис. 64) между линией наибольшего наклона и ее фронтальной проекцией равен углу наклона плоскости к фронтальной плоскости проекций. Поэтому линия наибольшего наклона характеризует угол наклона плоскости к фронтальной плоскости проекций.

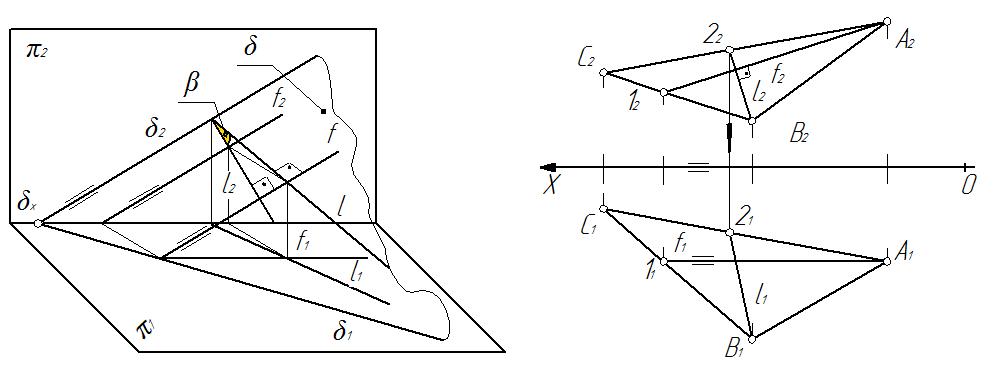
Рис. 64 Рис. 65

Алгоритм построения линии наибольшего наклона (рис. 65).

1. В заданной плоскости проводится фронталь f.

2. Используя теорему о прямом угле, на второй проекции плоскости, строится проекция линии наибольшего наклона f₂(В₂2₂)^f₂(A₂1₂).

3. По принадлежности прямой плоскости достраивается недостающая проекция l₁ линии наибольшего наклона.

Следует отменить, что все линии наибольшего наклона параллельны между собой и перпендикулярны фронтальному следу плоскости.

7.2. Построение линии пересечения проецирующей плоскости
с плоскостью общего положения

Пусть пересекаются две плоскости. Одна из плоскостей проецирующая, а другая плоскость общего положения. Необходимо определить линию пересечения этих плоскостей.

Известно, что на эпюре одна из проекций проецирующей плоскости вырождается в прямую. Используем этот характерный признак для определения линии пересечения плоскостей.

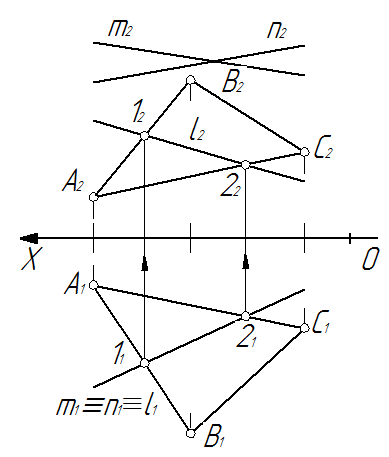Рис. 66

Так как линия пересечения плоскостей принадлежит проецирующей плоскости, то тогда ее проекция совпадет с вырожденной проекцией проецирующей плоскости. Следовательно, решение задачи по определению линии пересечения плоскостей сводится к определению недостающей проекции этой прямой, как прямой принадлежащей плоскости общего положения.

Рассмотрим решение такой задачи на примере (рис. 66).

Дано: плоскость общего положения α(∆АВС) и горизонтально-проецирующая плоскость.

Определить линию пересечения плоскостей α∩β=l.

Решение

1. Так как β(m∩n) ^ π₁=>l₁≡m₁≡n₁.

2. l₁∩A₁B₁=1₁ и l₁∩A₁С₁=2₁.

3. 1ÌAB=>1₂ÌA₂B₂ и 2ÌAС=>2₂ÌA₂С_2.

4. Через полученные точки 1₂ и 2₂ строится l₂(1₂2₂).