Перпендикулярность и параллельность плоскостей

Перпендикулярность плоскостей. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Исходя из этого определения для построения перпендикулярных плоскостей необходимо вначале построить перпендикуляр к плоскости, а затем используя его и способы задания плоскостей достроить перпендикулярную плоскость (рис. 75).

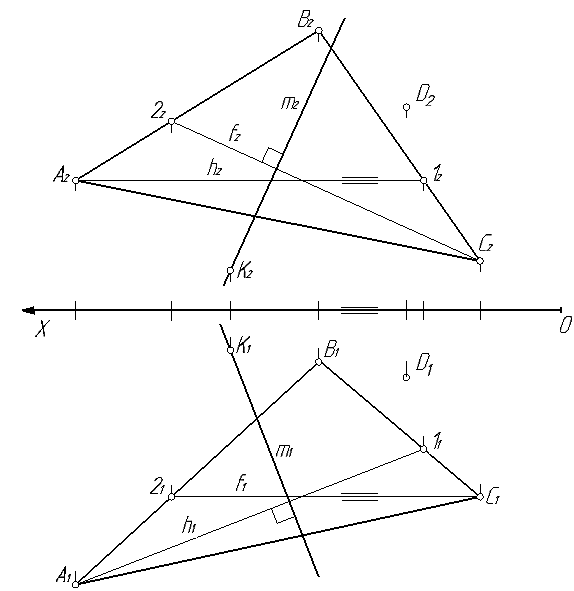
Рис. 75

На рис. 75 плоскость β(m,D)⊥α(∆ABC) так как прямая (m⊂β)⊥α.

Параллельность плоскостей. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны между собой. Исходя из этого для построения параллельных плоскостей достаточно использовать характерный признак параллельности прямых и способы задания плоскостей (рис. 76).

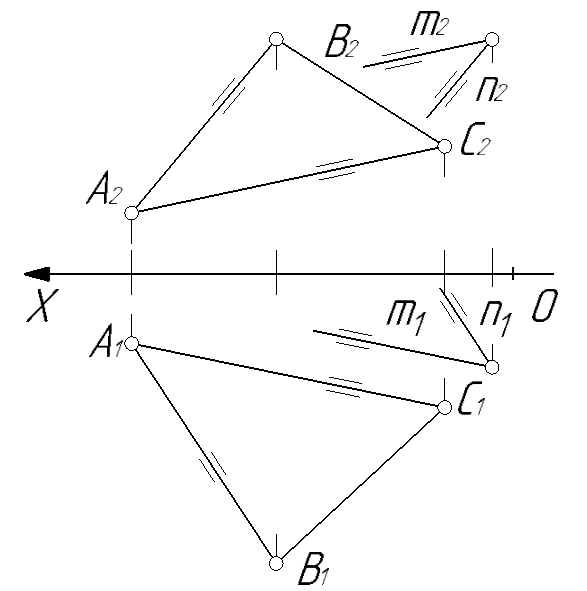
Рис. 76

На рис. 76 плоскость α(∆АВС)∥β(m∩n), так как m∥AC, а n∥AB.

Контрольные вопросы

1. Как строится линия пересечения двух плоскостей общего положения.

2. Как определяется видимость при пересечении двух плоскостей общего положения?

3. Покажите на примере построение прямой, параллельной плоскости общего положения.

4. Расскажите как строится плоскость проходящая через заданную точку и перпендикулярно заданной прямой.

5. Расскажите алгоритм построения перпендикуляра к плоскости, проходящего через заданную точку.

6. Сформулируйте, как построить на эпюре плоскость, перпендикулярную другой плоскости общего положения.

7. Сформулируйте, как построить на эпюре плоскость, параллельную другой плоскости.