Характеристика прямых

Все прямые пространства подразделяются на прямые общего и частного положений.

Прямая общего положения. Прямая общего положения не параллельны и не перпендикулярны ни одной из плоскостей проекций.

Примеры таких прямых показаны на рис. 28 и 29.

Особенностью изображения этих прямых является то, что на эпюре проекции прямой составляют с осями проекций произвольные углы и поэтому величина каждой проекции меньше истинной величины самой прямой (рис. 28).

Прямая частного положения. Прямые, параллельные или перпендикулярные плоскостям проекций называют прямыми частного положения.

Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня.

1. Прямые, параллельные горизонтальной плоскости проекций; называют горизонтальными или горизонталями h (рис. 30).

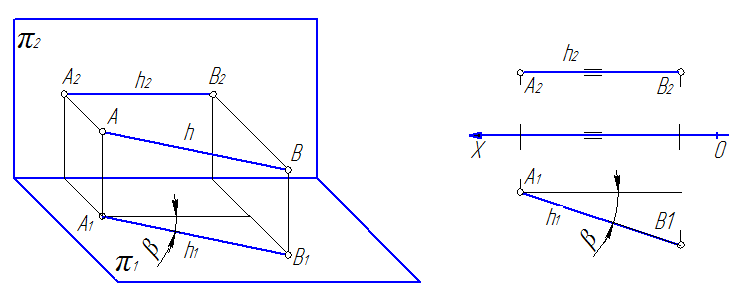
Рис. 30

Характерным признаком таких прямых на эпюре является то, что их фронтальные проекции параллельны оси 0Х.

2. Прямые, параллельные фронтальной плоскости проекций; называют фронтальными или фронталями f (рис. 31).

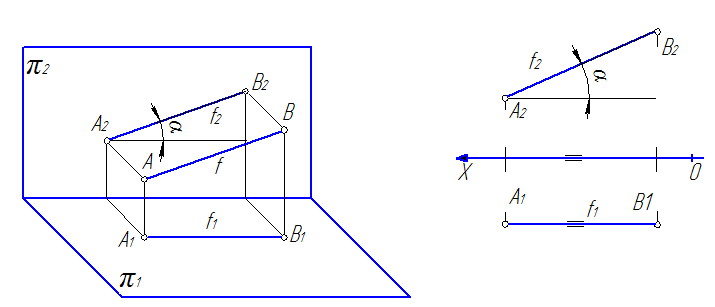
Рис. 31

Характерным признаком таких прямых на эпюре является то, что их горизонтальные проекции параллельны оси 0Х.

3. Прямую, параллельную профильной плоскости проекций, называют профильной р (рис. 32).

Характерным признаком таких прямых на эпюре является то, что их горизонтальные и фронтальные проекции перпендикулярны оси 0Х.

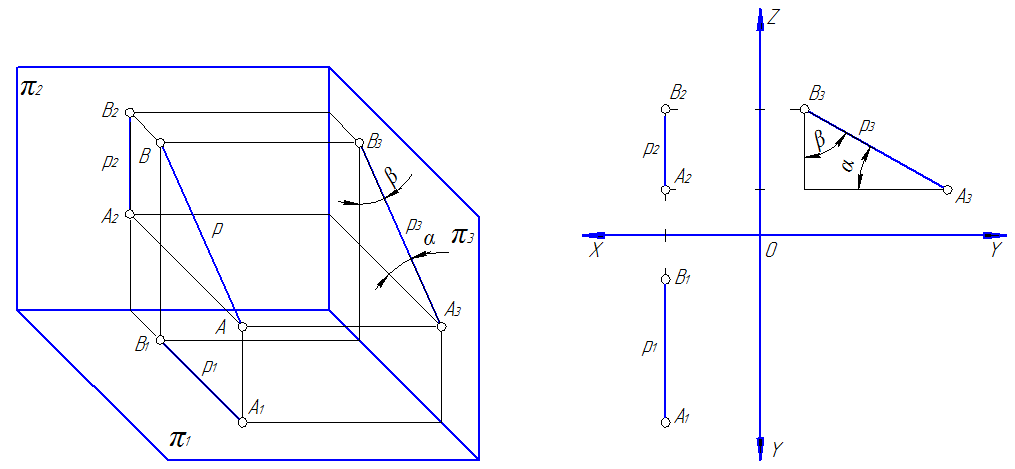
Рис. 32

Следует отметить, что каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона a и b, которые эта прямая образует с двумя другими плоскостями проекций, так же будут проецироваться на эту плоскость без искажения.

Так на рис. 30 проекция [A₁B₁]=[AB], а угол b – угол наклона отрезка [AB] к плоскости π₂. На рис. 31 проекция [A₂B₂]=[AB], а угол a – угол наклона отрезка [AB] к плоскости π₁. На рис. 32 видно, что все проекция [A₂B₂]=[AB], а углы a и b – углы наклона отрезка [AB] к плоскостям π₁ и π₁ соответственно.

Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевыми горизонталями, нулевыми фронталями и нулевыми профильными прямыми.

Прямые, перпендикулярные к одной из плоскостей проекций называются проецирующими:

1) горизонтально-проецирующая – прямая l, перпендикулярная к горизон­тальной плоскости проекций (рис. 33);

2) фронтально-проецирующая – прямая m, перпендикулярная к фронтальной плоскости проекций (рис. 34);

3) профильно-проецирующая – прямая n, перпендикулярная к профильной плоскости проекций (рис. 35).

На рис. 33 34 и 35 видно, что проекции прямых, перпендикулярных к плоскостям проекций, на этих плоскостях представляют собой точки, а на тех плоскостях, которым прямые параллельны, проекции прямых будут перпендикулярны к осям и равны по величине самим прямым.

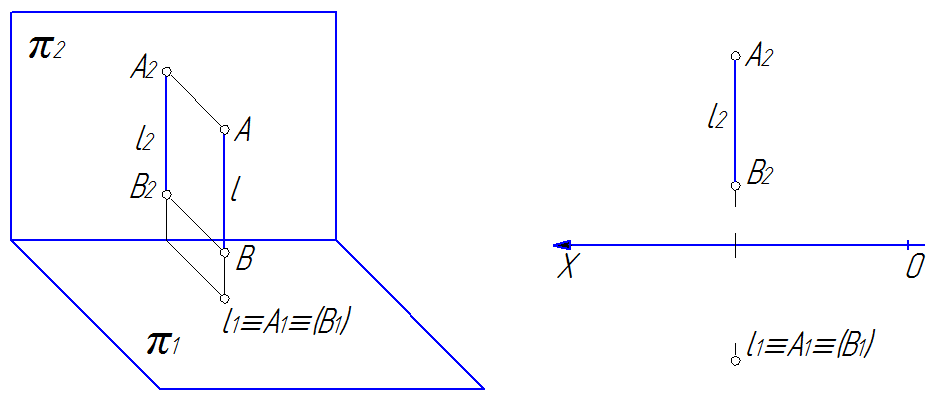
Рис. 33

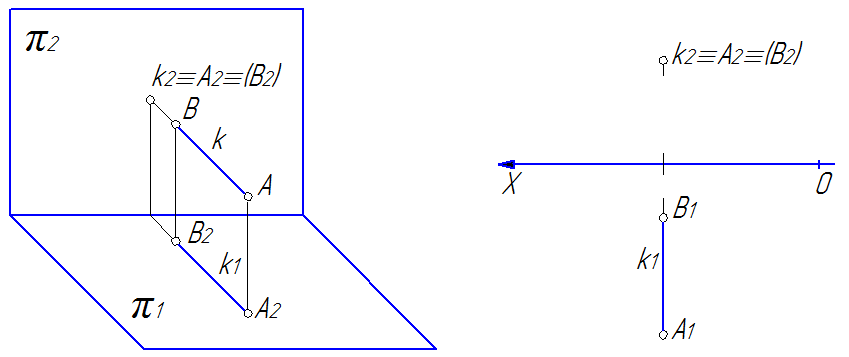
Рис. 34

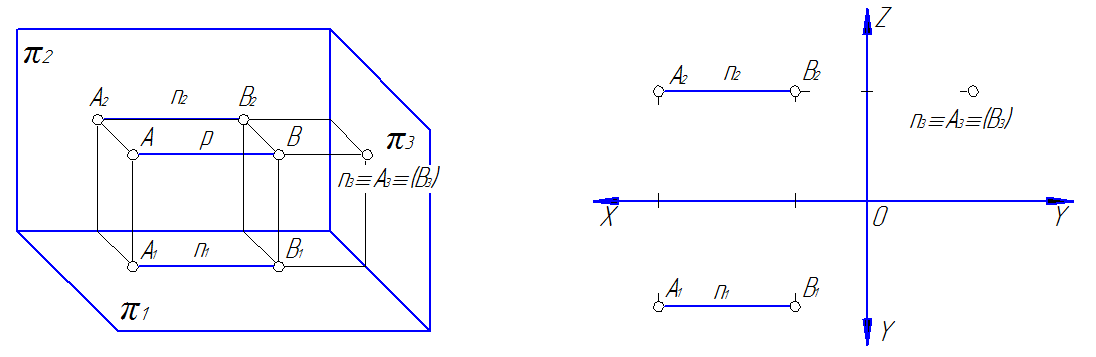
Рис. 35