Традиционные методы экономической статистики.
В группу методов экономической статистики включают:
· метод средних величин;
· метод группировок;
· элементарные методы обработки расчетных данных;
· индексный метод.
Метод средних величин заключается в обобщении, т.е. замене множества индивидуальных значений признаков в совокупности – на значение средней величины, характеризующей всю совокупность.
В любой совокупности экономических явлений наблюдаются различия между отдельными единицами этой совокупности. Одновременно в них есть что-то общее, что объединяет их и позволяет включить в данную совокупность. Средняя величина обобщает качественно однородные значения признака и, следовательно, является типической характеристикой признака в данной совокупности. Например, среднемесячная заработная плата, средняя цена тонны цемента и т.д. Средняя величина не является постоянной, она изменяется – растет или уменьшается.
В процессе анализа ФХД используются:
· средняя арифметическая (простая и взвешенная);
· средняя геометрическая;
· средняя гармоническая;
· средняя хронологическая.
Средняя простая арифметическая – это такое среднее значение признака, при исчислении которого общий объем признака в совокупности не меняется, т.е. средняя арифметическая – это среднее слагаемое. Объем признака распределяется поровну между всеми единицами. Если же объем совокупности велик и представляет собой ряд распределения, используют средневзвешенную арифметическую.
Средняя геометрическая применяется при изучении темпов роста, она позволяет сохранить неизменной не сумму совокупности, а произведение индивидуальных величин. Применяется, когда известны промежуточные значения темпов роста в каком-то периоде, и, необходимо определить темп роста в целом на конец периода. Средняя геометрическая дает правильный ответ, когда надо определить значение экономической величины, которое было бы качественно равно удалено как от ее максимального значения, так и от минимального значения.
Средняя гармоническая применяется в случаях, когда необходимо, что бы при усреднении оставалась неизменной сумма величин обратных индивидуальным значениям признака.
Средняя хронологическая – применяется для усреднения моментных показателей.
Метод группировки данных применяется с целью изучения структуры совокупности или взаимосвязей между компонентами.
В анализе ФХД организации используется в основном два вида группировок: структурные и аналитические.
Структурные группировки предназначены для изучения структуры и состава совокупности, происходящих в ней сдвигов относительно выбранного варьирующего признака. Группировки оформляются, как правило, в виде таблицы, в подлежащем которой находится группировочный признак, а в сказуемом – показатели, характеризующие структуру совокупности либо в динамике, либо в пространстве.
Аналитические группировки предназначены для изучения взаимосвязей между двумя и более показателями, характеризующими совокупность. Один из показателей при этом рассматривается как результативный, а остальные – как факторные.
При построении группировок нужно очень осторожно и серьезно относится к делению совокупности на группы. Например, группировка предприятий по фондовооруженности труда.
По данным анализа делаем объективный вывод, что выработка напрямую зависит от фондовооруженности и чем выше Ф/В, тем выше производительность труда.
Элементарные методы обработки расчетных данных. При изучении совокупности изучаемых величин помимо средних величин используют и другие характеристики.
Таблица 3 - Зависимость выработки от фондовооруженности труда (млн. руб.)
| Группы предприятий по фондовооруженности | Количество предприятий | Средний уровень Ф/В по группе | Средняя выработка 1го рабочего |
| до 3,5 | 3,25 | 4,45 | |
| от 3,6-4,0 | 3,76 | 5,10 | |
| от 4,1-4,5 | 4,23 | 5,73 | |
| свыше 4,5 | 4,75 | 6,30 |
При изучении больших массивов данных обычно интересуются двумя аспектами:
· величинами, которые характеризуют ряд значений, как целого;
· величинами, которые описывают различия между членами совокупности.
Все средние относятся к первой группе показателей, т.к. характеризуют совокупность в целом. Кроме тог, в качестве показателей общности используются следующие величины: середина интервала, мода, медиана.
Середина интервала: 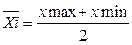 .
.
Мода – такое значение признака, которое среди всех его значений встречается наиболее часто. Если в совокупности два признака встречаются наиболее часто – то совокупность бимодальная. Если в совокупности наиболее часто встречаются более двух признаков – то совокупность мультимодальная.
Медиана – такое значение изучаемой величины, которое делит анализируемую совокупность на две равные величины, в которых количество членов с большими значениями, чем медиана, равно количеству членов со значениями, меньше медианы.
Индексный метод. Важное условие, которое надо соблюдать при анализе – необходимость обеспечения сопоставимости показателей. Сопоставимость достигается тем, что сравниваемые показатели приводятся к единой базе по уровню факторов. Например, если несопоставимость показателей вызвана разным уровнем стоимостной оценки, то для нейтрализации данного фактора их уровень выражают в одних и тех же ценах.
Данная проблема решается с помощью индексов. С помощью индексов в АФХД решаются и другие задачи, такие как:
· выявление роли отдельных факторов в изменении результативного показателя;
· оценка влияния изменения структуры совокупности на динамику.
С помощью индексов проводят сравнение с планом, с предыдущим периодом, в динамике, в пространстве. Индекс представляет собой отношение двух состояний какого-либо признака.
Индекс может быть простым (частным, индивидуальным), если исследование ведется без учета связи признака с другими признаками изучаемых явлений.
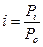 ,
,
где Pi и Po – сравниваемые состояния признака.
Индекс называется аналитическим (общий, агрегатный), если исследуемый признак берется не изолированно от других признаков этого явления. Аналитический индекс всегда состоит из двух компонентов: признака, который исследуется и весового признака.
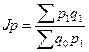 или
или 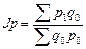 ,
,
где q0 и q1- весовой признак.
При проведении анализа аналитику необходимо сначала выбрать исследуемый признак, а затем – период, на уровне которого берется признак – вес. Различают базисные и цепные индексы. Базисный индекс рассчитывается по отношению к определенной базе. Цепной – рассчитывается к предыдущему периоду.
3. Стохастическое моделирование или математико-статистические методы изучения связей являются дополнением и углублением детерминированного анализа.
Детерминированное моделирование факторных систем ограничено длиной факторного поля прямых связей.
При недостаточном уровне знаний о природе прямых связей того или иного показателя хозяйственной деятельности часто необходим иной подход к познанию объективной действительности. Стохастический анализ выступает в качестве инструмента углубления детерминированного анализа факторов, по которым нельзя построить детерминированную модель.
Для изучения стохастических, вероятностных взаимосвязей применяется корреляционно-регрессивный метод анализа. Его применение позволяет количественно оценить тесноту связи между изучаемыми величинами, дать оценку доли влияния факторов на результативный показатель, описать форму взаимосвязи, определить прогнозное значение совокупного показателя при изменении факторного. Необходимость включения стохастического моделирования в АФХД организации зависит от значимости решаемых задач.
Можно выделить следующие наиболее типичные классы задач АФХД, для решения которых применяются методы стохастического моделирования:
· изучение наличия, направления и интенсивности связей показателей хозяйственной деятельности;
· ранжирование и классификация факторов экономических явлений;
· выявление аналитической формы связи между показателями;
· выявление наиболее информативных (обобщающих) показателей хозяйственной деятельности;
· определение структурных сдвигов в совокупности объектов анализа;
· нахождение общих закономерностей в функционировании объекта;
· построение усредненных нормативов хозяйственной деятельности.
По характеру перечисленных задач можно судить, что методы стохастического моделирования, при количественном изменении, применяются при условии наличия достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей.
Исполнение стохастических моделей в экономике, в отличие от исполнения их в технике, имеет определенные трудности. В технике эксперимент можно повторить, в экономике – нельзя. Это приводит к дискуссии о правомерности использования стохастических методов при построении факторных моделей в анализе ФХД организации, т.к. стохастическая (корреляционная) связь - это неполная вероятная зависимость между показателями, которая проявляется только в массе наблюдений.
Математический аппарат решения задач стохастического моделирования подробно описан в учебниках по теории статистики.
4. Методы теории принятия решенийвключают:
· метод построения дерева решений;
· линейное программирование;
· анализ чувствительности.
Метод построения дерева решений полезен в различных областях деятельности менеджеров, например, в управленческом учете, при составлении бюджета капиталовложений и особенно в анализе на рынке ценных бумаг.
Метод линейного программирования наиболее распространен в прикладных экономических исследованиях. Он позволяет хозяйствующему субъекту дать обоснование наилучшему решению в условиях более или менее жестких ограничений, касающихся доступных для организации ресурсов. С помощью линейного программирования в АФХД решается ряд задач, в первую очередь относящихся к процессу планирования деятельности. Он позволяет отыскать оптимальные параметры выпуска продукции и способы наилучшего использования имеющихся ресурсов.
Анализ чувствительности применяется в условиях неопределенности. Очень часто этот метод используется при анализе инвестиционных проектов, а также при прогнозировании величины чистой прибыли организации. Этот анализ позволяет определить силу реакции результативного показателя на изменение факторных.
5. Методы финансовых вычислений наиболее часто применяются для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, ссудозаемных операциях, в оценке бизнеса.
Финансовые вычисления базируются на понятии временной стоимости денег. В условиях инфляции денежные ресурсы, как и любой другой вид активов, должны обращаться, и по возможности быстрее.
Временную ценность денег можно рассматривать в двух аспектах:
Во-первых – деньги с течением времени обесцениваются;
Во-вторых – это связанно с обращением капитала.
Например:
1) Инфляция составляет 20% в год. Предприятие имеет свободные наличные деньги 20 тыс. руб. это означает, что к концу года их покупательная способность снизится до 16,66 т.р.
2) Предприятие имеет возможность участвовать в некоторой операции, которая через два года принесет доход 100 000 руб. предлагается выбрать вариант: или получить через год 50 тыс. и на второй год 50 тыс., или через два года сразу 100 тыс. Конечно же, первый вариант явно предпочтительней.
Проблема «деньги-время» не нова, поэтому уже разработаны удобные модели и алгоритмы, позволяющие ориентироваться в истинной цене доходов с позиции текущего момента.
Логика построения основных алгоритмов не сложна. Например, дать в долг какую-то сумму (So) и ожидать возврат ее с приростом (S1) , но как его рассчитать. Абсолютные показатели не подходят, т.к. нет в них сопоставимости. Поэтому пользуются специальным коэффициентом – ставкой, которая рассчитывается отношением приращения исходной суммы к базовой величине.
В финансовых вычислениях применяются такие названия коэффициентов:
§ Процентная ставка, процент, рост, ставка процента, норма прибыли, доходность 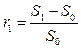
§ Учетная ставка, дисконтная ставка, дисконт
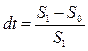
Эти два показателя связанны, зная один показатель, можно рассчитать другой 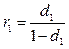 ; или
; или 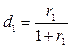 . Показатели могут выражаться либо в долях единиц, либо в процентах.
. Показатели могут выражаться либо в долях единиц, либо в процентах.
Известны две схемы дискретного начисления: схема простых процентов; схема сложных процентов.
Дата добавления: 2017-08-01; просмотров: 518;
