Статистические методы оценки качества

В процессе контроля и анализа качества электронных средств (ЭС) мы делаем выводы относительно генеральной совокупности. Эти выводы мы делаем по результатам контроля и исследования одной или нескольких выборок. В данном случае выборочную характеристику называют оценкой генеральной характеристики. А генеральную характеристику, определяемую с помощью данной оценки, называют оцениваемым параметром. В данном случае характеристики положения ( 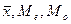) для выборки называют точечными оценками. А математическое ожидание М(х) для генеральной совокупности называют точечным оцениваемым параметром. Характеристики рассеивания для выборки [(S²(S)] называют интервальной оценкой. А характеристики рассеивания для генеральной совокупности [s (s²)] называют интервальными оцениваемыми параметрами.

Для случая нормального (гауссовского) закона распределения значения параметра качества 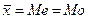. Для того, чтобы на основании оценки можно было бы сделать статистический вывод о качестве всей продукции (генеральной совокупности), необходимо, чтобы оценка была состоятельной, несмещенной, эффективной и достаточной.

Состоятельной является оценка, если при неограниченном возрастании объема выборки значение оценки сходится по вероятности к значению оцениваемого параметра. Обозначим через 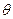значение оцениваемого параметра качества генеральной совокупности, а значение его оценки – через 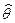, то в случае состоятельной оценки можно сказать, что если объем выборки n ® N, то вероятность того, что разность между значениями оценки 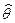и оцениваемого параметра 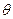меньше сколь угодно малой наперед заданной величины d, будет равна 1. В математике записывается следующим образом:

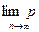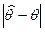( <s) =1.

Если значение оцениваемого параметра (а следовательно, и оценки, ибо выборка берется из рассматриваемой генеральной совокупности) имеет нормальный закон распределения, то точечные оценки ( 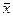, Ме, Мо) будут состоятельными оценками М(х), и интервальной оценки s(s²) будут состоятельными оценками s(s²).

Несмещенной является такая оценка, математическое ожидание которой равно значению оцениваемого параметра, т.е.

.

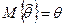Если точечные оценки ( 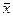, Мо, Ме) являются несмещенными оценками М(х), то интервальные оценки s(s²) будут смещенными оценками интервальных оцениваемых параметров s и s².

Эффективной является оценка, дисперсия которой относительно оцениваемого параметра качества генеральной совокупности не больше дисперсии любой другой оценки относительно этого же оцениваемого параметра. Дисперсия 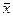относительно М(х) в случае нормального распределения случайной величины имеет следующее выражение:

,

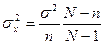где s² – дисперсия случайной величины х генеральной совокупности; N – объем генеральной совокупности; n – объем выборки.

Для случая, когда N>>n, то имеем 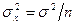. Если же в качестве оценки М(х) взять медиану, то для нормального закона распределения случайной величины х генеральной совокупности дисперсия медианы относительно М(х) имеет следующее выражение:

.

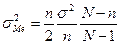Для случая, когда N>>n, имеем

.

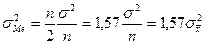Таким образом, при использовании в качестве оценки медианы потребовалось бы на 57% больше наблюдаемых значений случайной величины, чем в случае .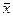

Достаточной оценкой является такая, которая содержит всю необходимую информацию об оцениваемом параметре генеральной совокупности.

Если при контроле качества распределение случайных значений контролируемого параметра качества подчиненного гауссовскому закону, то для получения статистических выводов достаточно проанализировать два параметра выборки: 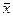и s²(s).