Расслаивание общей изменчивости с помощью дисперсионного анализа

Общая (суммарная) изменчивость статистических данных, которая характеризует качество изделия на различных этапах его жизненного цикла состоит из случайной изменчивости и систематической изменчивости. Источниками случайной изменчивости являются некачественные материалы, низкая квалификация исполнителей и т.д.

Источником систематической изменчивости является применяемое в технологическом процессе оборудование.

В то же время дисперсия внутри выборки 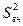характеризуется в основном случайной изменчивостью, а дисперсия между выборками 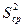- систематической изменчивостью. Сравнивая дисперсию, обусловленную только одним каким-либо фактором, с общей дисперсией с помощью дисперсионного анализа, можно решить вопрос о значимости влияния этого фактора на общую дисперсию. В качестве критерия значимости используется критерий Фишера F. Если F-критерий подтвердит превалирующее влияние той или иной изменчивости, то это значительно сократит поиск нарушений технологического процесса.

Пример. Было взято 4 выборки транзистора. В каждой выборке по 5 транзисторов. Были измерены значения коэффициентов усиления по току. Выборки были взяты из генеральной совокупности, подчиняющейся гауссовскому закону распределения.

М(х)=β=50

σ=10

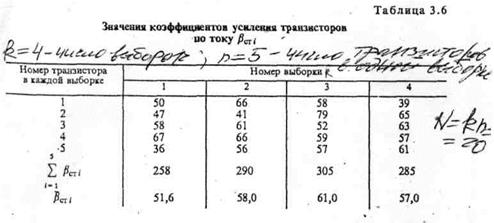
Значение коэффициентов усиления приведено в таблице 3.6.

Общее число транзисторов N=k·n=20.

Основные статистические характеристики определим методом непосредственного вычисления. β обозначим через x_i.

Общее среднее значение коэффициента усиления:

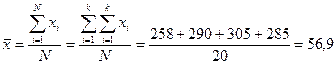
Найдем среднее значение от средних значений для всех выборок.

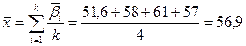
Общее среднее равно среднему значению от средних значений всех выборок.

Определим дисперсию.

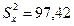
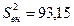
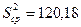
Теперь можно определить причину изменчивости средних значений. Для этого воспользуемся критерием Фишера:

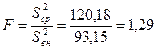
Определим табличное значение числа степеней свободы ν.

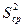ν₁=k-1=4-1=3

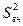ν₂=N-1=20-4=16

F_табл=3,24

F< F_табл

Следовательно, расхождение оценок дисперсии генеральной совокупности случайно, несмотря на то, что ^> .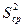

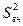Диаграмма разброса (поле корреляции)

Диаграмма разброса применяется для исследования зависимости (корреляции) между двумя видами данных. С помощью нее очень удобно наблюдать за влиянием различных факторов на параметры качества изделия. В этом случае по оси абсцисс откладывается начальное значение изучаемого параметра качества, а по оси ординат – те же значения параметра качества, но после воздействия.

Значение параметра качества каждого изделия до и после эксперимента будет обозначаться точкой в системе указанных координат. Следовательно, все n изделий, подвергшихся эксперименту, будут изображаться разбросанными по координатному полю точками. Эта совокупность точек образует диаграмму разброса.

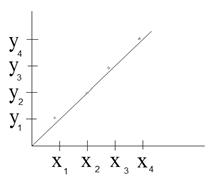
Рис. 10. Диаграмма разброса

Проведем биссектрису. Если все точки лягут на биссектрису, значит, параметр качества не изменился. Следовательно, данный фактор не влияет на данный параметр качества.

Пример. Рассмотрим влияние термообработки интегральных микросхем при Т=120 °С (t=24 ч.) на изменение обратного тока p-n-перехода. n=25.

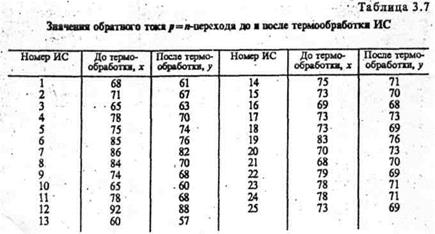
Значение тока находится в таблице 3.7.

По таблице находят максимальное и минимальное значения для X и Y.

x_max=92

x_min=60

y_max=88

y_min=57

Строим график y(х). При этом длину осей делают почти равной разности между их максимальными и минимальными значениями. Получается почти квадрат. На график наносятся данные в порядке измерений и точки диаграммы разброса.

Для определения вида связи используют метод наименьших квадратов.

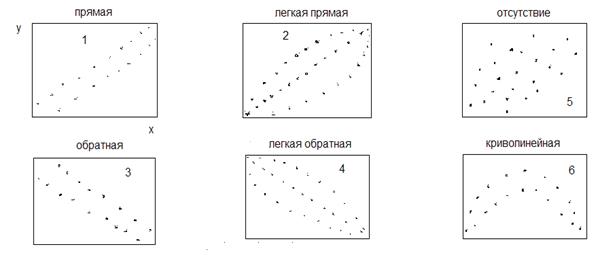
Рис. 11. Виды корреляции

На диаграмме (11.1) просматривается прямая корреляции между X и Y. В этом случае, контролируя причинный фактор X, можно управлять значением параметра качества Y.

На рисунке 11.2 приведен пример легкой прямой. При увеличении Х растет Y, но разброс Y велик по отношению к определенному значению Х. Контролируя причинный фактор X, можно до некоторой степени держать под контролем характеристику Y. В данном случае надо иметь ввиду и другие факторы, оказывающие влияние на фактора Y.

На рисунке 11.5 приведен пример отсутствия корреляции. Здесь нужно продолжить поиск факторов, коррелирующих с фактором Y. При этом фактор Х исключается. Между параметрами X и Y возможны случаи криволинейной корреляции (рис. 11.6). Диаграмма разброса делится на участки, имеющие прямолинейный характер. После этого исследуют каждый участок.

Степень корреляционной связи между X и Y может быть оценена либо с помощью коэффициента корреляции (для прямолинейной корреляции) или корреляционного отношения (для криволинейной корреляции).

Диаграмма Парето

Данная диаграмма названа в честь итальянского экономиста Парето. Диаграмма Парето позволяет распределить усилие при решении возникающих проблем качества. Ее построение начинают с классификации возникающих проблем по отдельным факторам. После этого начинают сбор и анализ статистического материала по каждому фактору.

В прямоугольной системе координат по оси абсцисс откладывают равные отрезки, рассматриваемые фактором. По оси ординат – величину их вклада в изучаемую проблему. При этом порядок расположения фактора таков, что влияние каждого последующего фактора, расположенного по оси абсцисс, уменьшается по сравнению с предыдущим фактором. В результате получится диаграмма в виде столбчатого графа, столбики которого соответствуют отдельным факторам. Высота столбиков уменьшается слева направо.

Построим гистограмму вкладов дефекта различных технологических операций.

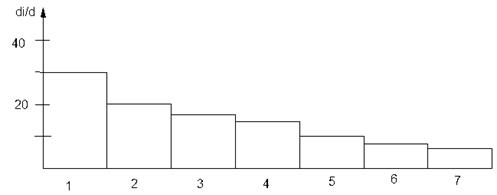
Рис. 12. Гистограмма вкладов дефекта различных технологических операций

По оси абсцисс отложим суммарное количество дефектов готовых ИМС, по оси ординат – относительную долю числа дефектов от рассматриваемого.

1 – припайка кристалла (26%);

2 – герметизация (22%);

3 – разладка выводов (19%);

4 – фотолитография (18%);

5 – осаждение диэлектрика (7%);

6 – диффузия (5%);

7 – металлизация (3%).

Суммируя последовательно высоту всех столбиков гистограммы, получим ломаную кумулятивную прямую, которую называют кривой Парето.

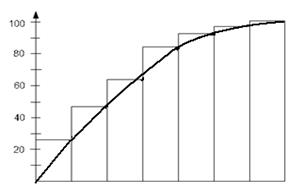
Рис. 13. Кривая Парето