Определение доверительных интервалов оценок генеральных характеристик

Для каждой статистической характеристики, вычисленной по результатам выборки, следует указывать точность оценки. Эта точность содержится в доверительном интервале. В этом случае замена генеральной характеристики ее оценкой делается с определенной достоверностью (доверительной вероятностью). Она характеризует степень нашего доверия к анализируемым результатам. Обычно достоверность, которую обозначим через Р, выбирается близко к единице (0,9; 0,95; 0,99). Она получается вычитанием из единицы величины уровня значимости коэффициентом риска β.

Строго говоря, достоверность– это вероятность того, что оцениваемый параметр лежит между доверительными границами.

В случае точечной оценки М(х) с помощью 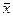для гауссовского закона распределения случайной величины Х эта взаимосвязь количественно определяется теоремой Ляпунова

Теорема: С вероятностью, равной Ф₁(a), можно утверждать, что при наличие в выборке объема n достаточно большого числа независимых (или слабо зависимых) случайных величин х_i, которая сравнительно мало отличаются друг от друга, разность между генеральными и выборочными средними арифметическими значениями будет лежать в пределах e, т.е. можно записать:

Р{- e £ М(х) - 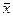£+ e} = Ф₁ (a),

В данном случае e = 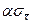- это точность оценки или половина поля допуска; величину 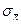выбираем либо по формулам, либо по таблицам относительно α.

Пусть имеется распределенная по закону Гаусса генеральная совокупность с математическим ожиданием М(х) и среднеквадратическим отклонением σ=e. Относительно разности М(х) - 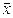можно с вероятностью, например, Ф₁(a) =0,95 утверждать, что она находится в интервале с границами 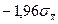и .

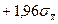Следовательно, можно записать следующее неравенство:

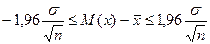
В ряде случаев величина σ не известна. В этом случае вместо σ используют стандартное отклонение.

.

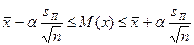Однако при замене интервального оцениваемого параметра s значением его оценки на практике встает другая задача: по выборочным характеристикам определить вероятность того, что неизвестное значение генерального среднего стандартного отклонения s будет лежать в заданных пределах e, т.е. нужно определить доверительные интервалы для s.

,

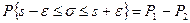где Р₁ и Р₂ – вероятности, определяемые по таблицам.

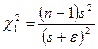и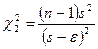

и для n₁=n₂=n – 1.

Пример. По 15 случайным независимым наблюдениям над величиной Х, имеющей в генеральной совокупности гауссовское распределение, найдено выборочное значение среднего квадратического отклонения, равное 6,7. Спрашивается: с какой вероятностью мы можем утверждать, что s заключено между 6,5 и 6,9?

Решение. Имеем e=0,2; n=15; S=6,7.

v=v₁=v₂=n – 1=14.

;

.

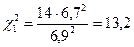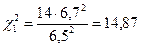Далее по таблице найдем значения Р₁ и Р₂.

Р₁=0,5111; Р₂=0,3875

Р₁- Р₂=0,1236

Следовательно, с точностью e=0,2 и вероятностью Р=0,1236 можно записать, что s»6,7. Если взять меньшую точность (т.е. большее значение e), то получилось соответственно и большее значение вероятности.