Оценка генеральной средней М(х) с помощью среднего
Значения выборки
Предположим, что значения параметра качества генеральной совокупности распределены по закону Гаусса.
1. Установление двустороннего критерия для среднего значения 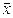 , когда s и М(х) известны.
, когда s и М(х) известны.
Предположим, что заказчику сдается партия электронных средств объемом N=10000 изделий. В соответствие с контрактом время безотказной работы должно быть не менее М(х)=14600 ч. При этом время отказа изделий t0=14000 ч.
Для определения этой партии установленным требованиям возьмем выборку n=100 изделий. Проведем ускоренные испытания на отказ. Получили:
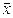 =14,591.
=14,591.
Для определения s возьмем s 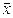 →s и
→s и 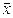 →
→ 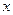 .
.
Тогда e=as.
e=14600-14000=600ч.
Выберем по таблице a=3,0, значит, e=3s. В результате получим:
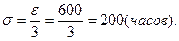
Р{ 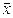 - e £ М(х) £
- e £ М(х) £ 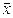 + e} = Ф1 (a),
+ e} = Ф1 (a),
где Ф1 (a) – вероятность того, что искомое значение М(х) будет лежать в указанных пределах.
Ф1 (a)=0,99
a=2,58
Определим минимальное значение М(х):
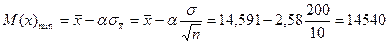 ч.
ч.
Вывод: следовательно, данная партия изделий соответствует требованиям контракта.
При контроле качества технологического процесса производства электронных средств средняя арифметическая 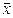 характеризует степень отлаженности технологического процесса. По величине
характеризует степень отлаженности технологического процесса. По величине 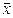 можно сделать вывод, что имеет место нарушение технологического процесса или нет.
можно сделать вывод, что имеет место нарушение технологического процесса или нет.
Пример. Имеется технологический процесс производства полупроводниковых микросхем. Производится контроль толщин пластин в процессе шлифовки. Распределение толщин подчиняется закону Гаусса. Допускается брак не более 10% пластин от всей партии. Толщина пластин после шлифовки должна быть М(х)=0,11 мм при среднеквадратическом отклонении s=0,01 мм.
Требуется определить величину допустимого отклонения e при контроле технологического процесса шлифовки пластин.
Установим объем выборки n=100.
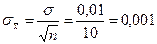 мм.
мм.
Ф1(a)=1-0,1=0,9.
Ф(a)=0,45
Следовательно, a=1,65.
e=a·s 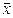 =1,65-0,001 =0,00165.
=1,65-0,001 =0,00165.
Допустимое абсолютное значение определим по формуле:
Р{ М(х) - e £ 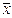 £ М(х) + e} = Ф1 (a).
£ М(х) + e} = Ф1 (a).
М(х) + e =0,11+1,65·0,001=0,11165 мм,
М(х) - e =0,11-1,65·0,001=0,10835 мм.
Следовательно, производственный процесс шлифовки пластин можно считать удовлетворительным, если среднее значение толщин 0,10835 £ 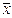 £ 0,11165. Такая проверка называется двухсторонней.
£ 0,11165. Такая проверка называется двухсторонней.
2. Установление двустороннего критерия для среднего значения 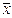 , когда М(х) известно, а s неизвестно.
, когда М(х) известно, а s неизвестно.
Рассмотрим случай малых выборок: n£10. В этом случае взаимосвязь между допустимыми пределами изменения 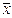 и вероятностью того, что разность между М(х) и
и вероятностью того, что разность между М(х) и 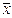 окажется в этих пределах, определяется с помощью критерия Стьюдента (или, иначе, t-распределения):
окажется в этих пределах, определяется с помощью критерия Стьюдента (или, иначе, t-распределения):
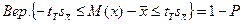 ,
,
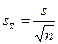 ;
;
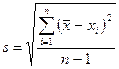 .
.
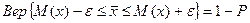 ,
,
где 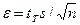 .
.
Задаваясь необходимой вероятностью (1 - Р), т.е. процентом выхода годных изделий, по таблице для критерия Стьюдента мы можем определить пределы изменения 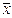 .
.
Пример. Возьмем исходные данные на операции шлифовки пластин, аналогичные приведенным в примере 1, т.е. М(х)=0,11 мм; должно быть отбраковано не более 10% изделий. Требуется определить величину e при условии, что объем выборки n=9, а толщины пластин (мм) в выборке следующие:
х1=0,112, х4=0,116, х7=0,109,
х2=0,116, х5=0,118, х8=0,114,
х3=0,108, х6=0,111, х9=0,107.
На основании имеющегося распределения:
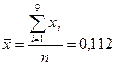 мм.
мм.
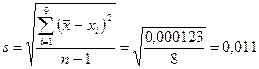 мм.
мм.
(1—Р)=1 – 0,9=0,1
v=n – 1=9-1=8.
Искомое значение tT равно 1,86.
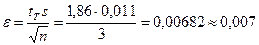 мм.
мм.
Следовательно, допустимыми границами изменения 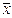 будут следующие значения:
будут следующие значения:
0,103 мм £ 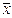 £ 0,117 мм.
£ 0,117 мм.
Если такие разбросы толщины не устраивают, то задача решается в обратном направлении. Задается допустимый разброс, рассчитываем tT и по значениям ищем вероятность Р.
По мере увеличения объема выборки разница между t – распределением и гауссовским распределением существенно уменьшается. Поэтому можно использовать гауссовское распределение только при небольших выборках.
Дата добавления: 2017-06-02; просмотров: 539;
