Коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади поверхности соприкасающихся слоев, при единичном градиенте скорости.

В системе СИ вязкость измеряется в Па·с, а в СГС - в пуазах (Пз): 1 Па·с = 10 Пз. Коэффициент вязкости жидкости зависит от природы жидкости (в частности, ее плотности) и температуры, уменьшаясь с ростом последней по экспоненциальному закону. Для более объективного учета характера взаимодействия молекул в непрерывных средах с разной плотностью, например, в жидкостях и газах, вводят понятие кинематического коэффициента вязкости.

Кинематический коэффициент вязкости равен отношению коэффициента η к плотности среды.

Для объяснения температурной зависимости коэффициента вязкости жидкостей необходимо учесть характер теплового движения составляющих их молекул. Оно, в основном, сводится к механическим колебаниям молекул около положений равновесия, которые в отличие от таковых в твердом теле изменяются с течением времени за счет переходов молекул в соседние положения с локальным минимумом потенциальной энергии. Для того, чтобы молекула жидкости перескочила из одного временного положения равновесия в другое, она должна нарушить связи со своими соседями, то есть преодолеть потенциальный барьер высотой DW. Величина DW называется энергией активации. Величина, обратная вероятности разрыва связи, определяется отношением энергии активации к тепловой энергии, равной произведению постоянной Больцмана k и абсолютной температуры T. С другой стороны, молекулы жидкости большую часть времени находятся около положения равновесия, и движущаяся масса жидкости увлекает соседние слои в основном за счет сил межмолекулярного взаимодействия, которые убывают с ростом температуры, и, следовательно, вязкость также убывает с ростом температуры.

Я. И. Френкель, исходя из характера теплового движения молекул в жидкостях, показал, что температурная зависимость вязкости жидкости имеет активационный характер и описывается выражением:

η = C·e ^DW/(k·T), (13.3)

где DW - энергия активации;

Т - абсолютная температура;

C - постоянная величина;

k - постоянная Больцмана, k = 1.38·10^-23 Дж/К;

е - основание натурального логарифма.

Применяя формулу Ньютона (13.2) для решения задач, связанных с течением жидкости, можно получить определенные количественные закономерности, которые используются для экспериментального определения коэффициента вязкости. Наиболее точными и распространенными методами определения вязкости являются:

	Метод Стокса,который основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы. На шарик, плотностью ρ и радиусом r , падающий в жидкости вязкостью η и плотностью ρ′ вертикально вниз со скоростью v, действуют три силы: сила тяжести, сила Архимеда и сила сопротивления.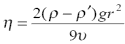
	Метод Пуазейля,который основан на измерении средней скорости установившегося течения жидкости в капилляре

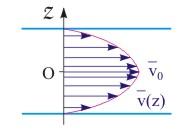
Рис. 13.2. Скорость движения слоев жидкости в горизонтальной трубе при ламинарном течении.

Течение реальных жидкостей и газов. Течение вязкой жидкости по трубам в зависимости от ряда условий может быть ламинарным (или слоистым) и турбулентным (или вихревым).

В случае ламинарного течения все молекулы жидкости движутся параллельно оси трубы и, находясь на одинаковом расстоянии от осевого центра трубы, имеют равные скорости (см. рис. 13.2). Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясьс ними.

Течение называется турбулентным (вихревым), если частицы жидкости переходятиз слоя в слой (имеют составляющие скоростей, перпендикулярные течению). Для турбулентного движения характерно наличие нормальной (перпендикулярной направлению течения жидкости) составляющей скорости движения молекул и резкий спад скорости течения при приближении к границам. Траектория движения молекул представляет собой сложную кривую линию.

Характер течения можно установить, пользуясь безразмерной величиной - числом Рейнольдса: 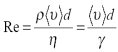(13.4)

γ = η /ρ— кинематическая вязкость; ρ — плотность жидкости; v — средняя по сечению трубы скорость жидкости; d— характерный линейный размер, например диаметр трубы. При Re ≤ 1000 наблюдается ламинарное течение, переход от ламинарноготечения к турбулентномупроисходит в области 1000 ≤ Re ≤ 2000, а при Re=2300 (для гладких труб) течение — турбулентное.

Лобовое давление и подъемная сила. Рассмотрим движение твердого тела относительно жидкости, находящейся в состоянии покоя в некоторой ИСО. Исходя из принципа относительности эта задача эквивалентна обтеканию неподвижного тела стационарным потоком жидкости.