Механические колебания и волны в упругих средах.

1. Колебания гармонические колебания

Колебанияминазываются движения или процессы, которые характеризуются опреде­ленной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электро­магнитные и др. Однако различные колебательные процессы описываются одинаковы­ми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы.

Колебания называютсясвободными, если они совершаются только под воздействием внутренних сил, действующих между элементами системы, после того как система выведена из положения равновесия внешними силами и предоставлена самой себе. Свободные колебания всегда затухающие колебания, ибо в реальных системах неизбежны потери энергии. В идеализированном случае системы без потерь энергии свободные колебания (продолжающиеся как угодно долго) называются собственными.

Простейшим типом свободных незатухающих колебаний являютсягармонические колебания –колебания, при которых колеб­лющаяся величина изменяется со временем по закону синуса (косинуса). Колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому.

Гармонические колеба­ния описываются уравнением, которое называется уравнением гармонических колебаний:

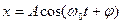, (14.1)

где А – амплитуда колебаний, максимальное значение колеблющейся величины х; 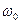– круговая (циклическая) частота собственных колебаний; 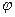– начальная фаза колебания в мо­мент времени t=0; 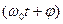–фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до -1, то х может принимать значения от +A до -А.

Время T , за которое система совершает одно полное колебание, называетсяпериодом колебаний.За время Т фаза колебания получает приращение 2π, т. е.

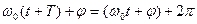, откуда 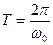. (14.2)

Величина 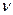, обратная периоду колебаний

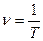(14.3)

т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (14.2) и (14.3) получим

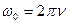. (14.4)

Единица частоты –герц (Гц): 1 Гц – частота, при кото­рой за 1с совершается одно полное колебание.

Системы, в которых могут происходить свободные колебания, называются осцилляторами. Какими же свойствами должна обладать система, чтобы в ней могли возникнуть свободные колебания? Механическая система должна иметь положение устойчивого равновесия, при выходе из которого появляется возвращающая сила, направленная к положению равновесия. Этому положению соответствуют, как известно, минимум потенциальной энергии системы. Рассмотрим несколько колебательных систем, удовлетворяющих перечисленным свойствам.