Возникновение подъемной силы в результате циркуляции воздуха вокруг твердого тела называется эффектом Магнуса.
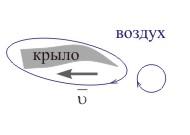
Рис. 13.4. Движение молекул воздуха около крыла самолета.
Наиболее характерным примером является наличие подъемной силы у крыла самолета при его движении относительно воздуха. Из-за характерной формы крыла вблизи его острой задней кромки в близлежащих слоях воздуха возникают вихревые воздушные потоки, причем направление вращения молекул происходит против часовой стрелки (см. рис. 13.4). Эти вихревые потоки постепенно нарастают и отрываются от крыла, но за счет наличия вязкого трения они заставляют вращаться по часовой стрелке вокруг поверхности крыла прилегающие к ней молекулы воздуха. Наличие циркуляции, обусловленной вязким трением, и приводит к возникновению подъемной силы.
Закон подобия.
Геометрическое, кинематическое, динамическое подобие.
Этап изучения зависимости интересующей величины от системы выбранных определяющих факторов может выполняться двумя путями: аналитическим и экспериментальным. Первый путь применим лишь для ограниченного числа задач и при том обычно лишь для упрощенных моделей явлений.
Другой путь, экспериментальный, в принципе может учесть многие факторы, но он требует научно обоснованной постановки опытов, планирования эксперимента, ограничения его объема необходимым минимумом и систематизации результатов опытов. При этом должно быть обосновано моделирование явлений.
Эти задачи позволяет решать так называемая теория подобия, т. е. подобия потоков несжимаемой жидкости.
Гидродинамическое подобие складывается из трех составляющих: геометрического подобия, кинематического и динамического.
Геометрическое подобие как известно из геометрии, представляет собой пропорциональность сходственных размеров и равенство соответствующих углов. Под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки, т. е. подобие русел (или каналов).
Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим эту величину через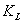 
.Эта величина одинакова для подобных русел I и II.
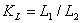
Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей:
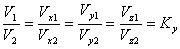
Где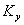 
– масштаб скоростей, одинаковый при кинематическом подобии.
Так как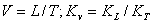 
(где T – время, 
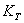–масштаб времени).
Из кинематического подобия вытекает геометрическое подобие линий тока. Очевидно, что для кинематического подобия требуется геометрическое подобие русел.
Динамическое подобие – это пропорциональность сил, действующих на сходственные объемы в кинематических подобных потоках и равенство углов, характеризующих направление этих сил.
В потоках жидкостей обычно действуют разные силы: силы давления, вязкости (трения), тяжести и др. Соблюдение их пропорциональности означает полное гидродинамическое подобие. Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, при котором соблюдается пропорциональность лишь основных, главных сил.
26.Идеальное упругое тело
Идеальное упругое тело или тело Гука, деформация которого прямо пропорциональна соответствующему напряжению.
Веществоидеального упругого тела непрерывно распределено по его объему. В случаях, когда нам придется выделять из этого тела бесконечно малые элементы, будем допускать, что и для этих элементов имеют место все те физические свойства, которыми обладает идеальное упругое тело.
Перечисленными свойствамиидеального упругого тела в большей или меньшей степени обладают и те естественные тела, с которыми нам приходится иметь дело при различных технических расчетах.
Простейшими реологическими уравнениями состоянияидеальных упругих тел и вязких жидкостей являются законы Гука и Ньютона. Линейные соотношения в них принимаются только при малых напряжениях и скоростях деформаций. Реальные эластомеры обладают и упругими, и вязкими свойствами в разных сочетаниях, которые зависят не только от деформации, но и от времени. Временная зависимость модуля упругости проявляется в релаксации напряжения.
Вследствие этого выводы теории упругости, относящиеся кидеальному упругому телу, можно с большой точностью применять к железу и стали. Конечно, при этом не будут учтены такие обстоятельства, как явление гистерезиса и влияние времени на деформацию г. Но для таких материалов, как железо и сталь, они не имеют существенного практического значения. Чугун, камни и дерево по своим свойствам больше отличаются от однородного идеального упругого тела и выводы теории упругости с гораздо меньшей точностью применимы к этим материалам. [5]
В стеклообразном состоянии полимеры близки по механическим свойствам кидеальному упругому телу они отличаются большим модулем упругости ( - 104 кгс / см2), практически независящим от времени действия силы и температуры.
Пока удлинения невелики, могут встречаться условия, при которых вещество ведет себя какидеальное упругое тело; в таких случаях для экспериментального определения модуля упругости могут быть применены уравнения ( I) и ( II), которыми пользовались иМейер, и Лотмар [1], и Ван дер Вик [2], исследовавшие целлюлозу.
Соответствие характера деформации виду напряжения подтверждает первая аксиома реологии: при всестороннем равномерном ( изотропном) сжатии все материальные системы ведут себя одинаково - какидеальные упругие тела. Это означает, что в таких разных по структуре телах, как металл, смола, вода, кислород ( газ), изотропное сжатие вызывает только упругую деформацию, а именно, уменьшаются размеры системы при сохранении ее формы и увеличивается плотность. При снятии нагрузки все параметры тела принимают первоначальные значения. Отсюда следует, что изотропное сжатие не позволяет выявить качественные различия в структуре тел.
Примером соответствия характера деформации виду напряжения является первая аксиома реологии: при всестороннем равномерном ( изотропном) сжатии все материальные системы ведут себя одинаково - какидеальные упругие тела.
При удалении внешних сил деформированное упругое тело возвращается к своему естественному состоянию, соответствующему данной температуре. Таким образом, естественное состояниеидеального упругого тела при данной температуре является устойчивой формой равновесия при этой температуре. Упругое тело обладает свойством накапливать в себе энергию в обратимой форме.
Подчеркнем, что выбор правильной модели для описания процесса динамического взаимодействия представляет собой очень сложную задачу. В связи с этим важным является понимание свойств границы как составного элемента моделиидеального упругого тела.
Для того чтобы лучше представить себе, что такое обобщенная модель Максвелла и непрерывный релаксационный спектр полимера, рассмотрим поведение обобщенной модели, которая деформируется с постоянной частотой со. С некоторым приближением можно считать, что все элементы модели с временами релаксации меньше 1 / со будут вести себя какидеальные упругие тела, деформация которых носит чисто обратимый характер.
Дата добавления: 2017-05-18; просмотров: 577;