Вращательное движение абсолютно твердого тела
Движение твердого тела называется вращательным, если во время движения все точки тела, расположенные на некоторой прямой, называемой осью вращения, остаются неподвижными (рис. 2.15).
Положение тела при вращательном движении принято определять углом поворота тела 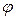 , который измеряется как двугранный угол между неподвижной и подвижной плоскостями, проходящими через ось вращения. Причем, подвижная плоскость связана с вращающимся телом.
, который измеряется как двугранный угол между неподвижной и подвижной плоскостями, проходящими через ось вращения. Причем, подвижная плоскость связана с вращающимся телом.
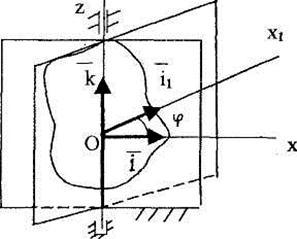
Рис. 2.15
Введем в рассмотрение подвижную и неподвижную системы координат, начало которых разместим в произвольной точке О оси вращения. Ось Oz, общую для подвижной и неподвижной систем координат, направим по оси вращения, ось Ох неподвижной системы координат направим перпендикулярно оси Oz таким образом, чтобы она лежала в неподвижной плоскости, ось Ох1 подвижной системы координат направим перпендикулярно оси Oz таким образом, чтобы она лежала в подвижной плоскости (рис. 2.15).
Если рассматривать сечение тела плоскостью, перпендикулярной оси вращения, то угол поворота φ можно определять как угол между неподвижной осью Ох и подвижной осью Ох1, неизменно связанной с вращающимся телом (рис. 2.16).
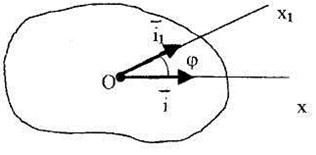
Рис. 2.16
Принято направление отсчета угла поворота тела φ против хода часовой стрелки считать положительным, если смотреть с положительного направления оси Oz.
Равенство φ = φ(t), описывающее изменение угла φ во времени, называется законом или уравнением вращательного движения твердого тела.
Быстрота и направление изменения угла поворота твердого тела характеризуются угловой скоростью. Абсолютное значение угловой скорости принято обозначать буквой греческого алфавита ω (омега). Алгебраическое значение угловой скорости принято обозначать 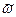 . Алгебраическое значение угловой скорости равно первой производной по времени от угла поворота:
. Алгебраическое значение угловой скорости равно первой производной по времени от угла поворота:
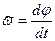 . (2.33)
. (2.33)
Единицы измерения угловой скорости равны единицам измерения угла, деленным на единицу измерения времени, например, град/мин, рад/ч. В системе СИ единица измерения угловой скорости рад/с, но чаще наименование этой единицы измерения записывается в виде 1/с.
Если 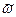 > 0, то тело вращается против хода часовой стрелки, если смотреть с конца оси координат, совмещенной с осью вращения.
> 0, то тело вращается против хода часовой стрелки, если смотреть с конца оси координат, совмещенной с осью вращения.
Если 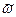 < 0, то тело вращается по ходу часовой стрелки, если смотреть с конца оси координат, совмещенной с осью вращения.
< 0, то тело вращается по ходу часовой стрелки, если смотреть с конца оси координат, совмещенной с осью вращения.
Быстрота и направление изменения угловой скорости характеризуются угловым ускорением. Абсолютную величину углового ускорения принято обозначать буквой греческого алфавита e (эпсилон). Алгебраическую величину углового ускорения принято обозначать 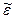 . Алгебраическая величина углового ускорения равна первой производной по времени от алгебраического значения угловой скорости или второй производной от угла поворота:
. Алгебраическая величина углового ускорения равна первой производной по времени от алгебраического значения угловой скорости или второй производной от угла поворота:
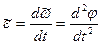 (2.34)
(2.34)
Единицы измерения углового ускорения равны единицам измерения угла, деленным на единицу измерения времени в квадрате. Например, град/с2, рад/ч2. В системе СИ единицей измерения углового ускорения является рад/с2, но чаще наименование этой единицы измерения записывается в виде 1/с2.
Если алгебраические значения угловой скорости и углового ускорения имеют один знак, то угловая скорость с течением времени увеличивается по модулю, а если разный, то уменьшается.
Если угловая скорость постоянна (ω =const), то принято говорить, что вращение тела равномерное. В этом случае
φ = 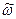 ·t + φ0 , (2.35)
·t + φ0 , (2.35)
где φ0- начальный угол поворота.
Если постоянно угловое ускорение (e=const), то принято говорить, что вращение тела равноускоренное (равнозамедленное). В этом случае
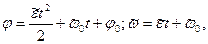 (2.36)
(2.36)
где 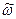 0- начальная угловая скорость.
0- начальная угловая скорость.
В остальных случаях для определения зависимости φ от 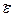 и
и 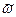 необходимо интегрировать выражения (2.33), (2.34) при заданных начальных условиях.
необходимо интегрировать выражения (2.33), (2.34) при заданных начальных условиях.
На рисунках направление вращения тела иногда показывают изогнутой стрелкой (рис. 2.17).
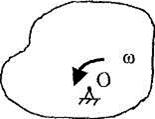
Рис. 2.17
Часто в механике угловая скорость и угловое ускорение рассматриваются как векторные величины 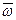 и
и 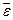 . Оба эти вектора направляются по оси вращения тела. Причем вектор
. Оба эти вектора направляются по оси вращения тела. Причем вектор 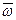 направляют в одну сторону с ортом, определяющим направление оси координат, совпадающей с осью вращения, если
направляют в одну сторону с ортом, определяющим направление оси координат, совпадающей с осью вращения, если 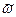 >0, и в противоположную, если
>0, и в противоположную, если
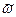 <0. Аналогично выбирают направление вектора
<0. Аналогично выбирают направление вектора 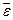 (рис. 2.18).
(рис. 2.18).
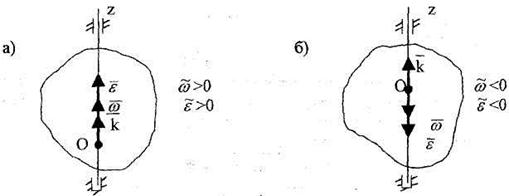
Рис. 2.18
При вращательном движении тела каждая из его точек (кроме точек, расположенных на оси вращения) перемещается по траектории, представляющей собой окружность с радиусом, равным кратчайшему расстоянию от точки до оси вращения (рис. 2.19).
Поскольку для окружности касательная в любой ее точке составляет угол 90° с радиусом, то вектор скорости точки тела, совершающего вращательное движение, будет направлен перпендикулярно радиусу и лежать в плоскости окружности, являющейся траекторией движения точки. Касательная составляющая ускорения будет лежать на одной прямой со скоростью, а нормальная будет направлена по радиусу к центру окружности. Поэтому иногда касательную и нормальную составляющие ускорения при вращательном движении называют соответственно вращательной и центростремительной (осестремительной) составляющими (рис. 2.19)
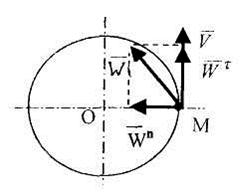
Рис. 2.19
Алгебраическая величина скорости точки определяется выражением
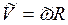 , (2.37)
, (2.37)
где R=OM – кратчайшее расстояние от точки до оси вращения.
Алгебраическая величина касательной составляющей ускорения определяется выражением:
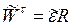 . (2.38)
. (2.38)
Модуль нормальной составляющей ускорения определяется выражением
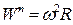 . (2.39)
. (2.39)
Вектор ускорения точки при вращательном движении определяется по правилу параллелограмма как геометрическая сумма касательной и нормальной составляющих. Соответственно модуль ускорения может быть определен по теореме Пифагора:
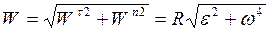 (2.40)
(2.40)
Если угловая скорость и угловое ускорение определены как векторные величины 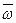 ,
, 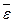 , то векторы скорости, касательной и нормальной составляющих ускорения могут быть определены по формулам:
, то векторы скорости, касательной и нормальной составляющих ускорения могут быть определены по формулам:
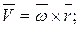
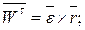
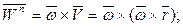
где 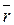 – радиус-вектор, проведенный в точку М из произвольной точки оси вращения (рис. 2.20).
– радиус-вектор, проведенный в точку М из произвольной точки оси вращения (рис. 2.20).
Решение задач на вращательное движение одного тела обычно не вызывает никаких трудностей. Используя формулы (2.33)-(2.40), можно легко определить любой неизвестный параметр.
Определенные сложности возникают при решении задач, связанных с исследованием механизмов, состоящих из нескольких взаимосвязанных тел, совершающих как вращательное, так и поступательное движение.
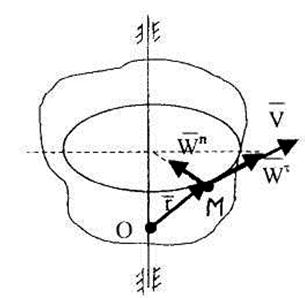
Рис. 2.20
Общий подход к решению подобных задач заключается в том, что движение от одного тела к другому передается через одну точку – точку касания (контакта). Причем у соприкасающихся тел равны скорости и касательные составляющие ускорений в точке контакта. Нормальные составляющие ускорения у соприкасающихся тел в точке контакта различны, они зависят от траектории движения точек тел.
При решении задач такого типа удобно в зависимости от конкретных обстоятельств использовать как формулы, приведенные в разделе 2.3, так и формулы для определения скорости и ускорения точки при задании ее движения естественным (2.7), (2.14) (2.16) или координатным (2.3), (2.4), (2.10), (2.11) способами. При этом если движение тела, к которому принадлежит точка, вращательное, траектория движения точки будет представлять собой окружность. Если движение тела прямолинейное поступательное, то траектория движения точки будет представлять собой прямую линию.
Пример 2.4.Тело вращается вокруг неподвижной оси. Угол поворота тела изменяется по закону φ = 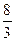 π·t 3рад. Для точки, находящейся на расстоянии OM=R=0,5 м от оси вращения, определить скорость, касательную, нормальную составляющие ускорения и ускорение в момент времени t1 =0,5 с. Показать направление этих векторов на чертеже.
π·t 3рад. Для точки, находящейся на расстоянии OM=R=0,5 м от оси вращения, определить скорость, касательную, нормальную составляющие ускорения и ускорение в момент времени t1 =0,5 с. Показать направление этих векторов на чертеже.
Рассмотрим сечение тела плоскостью, проходящей через точку О перпендикулярно оси вращения (рис. 2.21). На этом рисунке точка О -точка пересечения оси вращения и секущей плоскости, точки Мо и M1-соответственно начальное и текущее положение точки М. Через точки О и Мо проведем неподвижную ось Ох, а через точки О и М1 - подвижную ось Ох1. Угол между этими осями будет равен
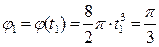 рад.
рад.
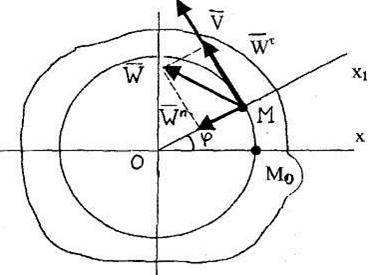
Рис. 2.21
Закон изменения угловой скорости тела найдем, продифференцировав закон изменения угла поворота:
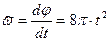
В момент t1 угловая скорость будет равна
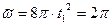 1/с.
1/с.
Закон изменения углового ускорения тела найдем, продифференцировав закон изменения угловой скорости:
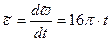
В момент t1 угловое ускорение будет равно
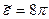 1/с2,
1/с2,
Алгебраические величины векторов скорости, касательной составляющей ускорения, модуля нормальной составляющей ускорения и модуля ускорения найдем по формулам (2.37), (2.38), (2.39), (2.40):
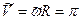 м/с;
м/с;
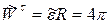 м/с2;
м/с2;
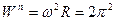 м/с2;
м/с2;
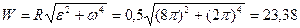 м/с2.
м/с2.
Так как угол φ1 >0, то откладывать его от оси Ох будем против хода часовой стрелки. А так как 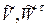 > 0, то векторы
> 0, то векторы 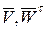 будут направлены перпендикулярно радиусу OM1 таким образом, чтобы мы видели их вращающимися против хода часовой стрелки. Вектор
будут направлены перпендикулярно радиусу OM1 таким образом, чтобы мы видели их вращающимися против хода часовой стрелки. Вектор 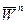 будет направлен по радиусу OM1 к оси вращения. Вектор
будет направлен по радиусу OM1 к оси вращения. Вектор 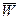 построим по правилу параллелограмма на векторах
построим по правилу параллелограмма на векторах 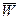 τ и
τ и 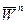 .
.
Пример 2.5. По заданному уравнению прямолинейного поступательного движения груза 1 х = 0,6t2 – 0,18 (м) определить скорость, а также касательную, нормальную составляющую ускорения и ускорение точки М механизма в момент времени t1, когда путь, пройденный грузом 1, равен s=0,2 м. При решении задачи будем считать, что проскальзывание в точке контакта тел 2 и 3 отсутствует, R2= 1,0 м, r2=0,6 м, R3=0,5 м(рис. 2.22).
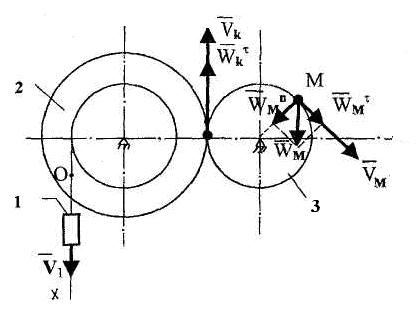
Рис. 2.22
Закон прямолинейного поступательного движения груза 1 задан в координатной форме. Определим момент времени t1, для которого путь, пройденный грузом 1, будет равен s
s = x(tl)-x(0),
откуда получим:
0,2 = 0,18 + 0,6t 12 - 0,18.
Следовательно,
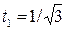 c.
c.
Продифференцировав по времени уравнение движения, найдем проекции скорости и ускорения груза 1 на ось Ох:
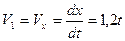 м/с;
м/с;
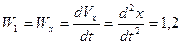 м/с2;
м/с2;
В момент t = t1 проекция скорости груза 1 будет равна:
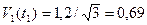 м/с,
м/с,
то есть будет больше нуля, как и проекция ускорения груза 1. Следовательно, груз 1 будет в момент t1 двигаться вниз равноускоренно, соответственно, тело 2 будет вращаться равноускоренно в направлении против хода часовой стрелки, а тело 3 - по ходу часовой стрелки.
Тело 2 приводится во вращение телом 1 через нить, намотанную на малый барабан. Поэтому модули скоростей точек тела 1, нити и поверхности малого барабана тела 2 равны, также равны будут и модули ускорений точек тела 1, нити и касательной составляющей ускорения точек поверхности малого барабана тела 2. Следовательно, модуль угловой скорости тела 2 можно определить как
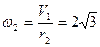 1/с.
1/с.
Модуль углового ускорения тела 2 будет равен
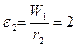 1/с 2.
1/с 2.
Определим модули скорости и касательной составляющей ускорения для точки К тела 2 - точки контакта тел 2 и 3:
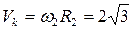 м/с,
м/с, 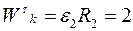 м/с2
м/с2
Так как тела 2 и 3 вращаются без взаимного проскальзывания, модули скорости и касательной составляющей ускорения точки К- точки контакта у этих тел будут равны.
Тело 3 совершает вращательное движение, поэтому модули скоростей и касательных составляющих ускорения всех точек его поверхности равны, поэтому:
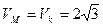 м/с; WM τ= WK τ=2м/c2.
м/с; WM τ= WK τ=2м/c2.
Модуль угловой скорости тела 3 будет равен:
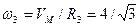 1/с.
1/с.
Модуль нормальной составляющей ускорения точки М будет равен:
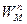 = ω32 R3 = 8/3м/с2.
= ω32 R3 = 8/3м/с2.
Модуль ускорения точки М будет равен
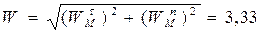 м/с2
м/с2
Так как тело 3 совершает вращательное движение, то вектор нормальной составляющей ускорения точки М 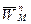 направим по радиусу к оси вращения – точке О3, векторы скорости
направим по радиусу к оси вращения – точке О3, векторы скорости 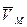 и касательной составляющей ускорения
и касательной составляющей ускорения 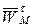 направим перпендикулярно радиусу в сторону вращения тела, так как тело 3 вращается равно ускоренно.
направим перпендикулярно радиусу в сторону вращения тела, так как тело 3 вращается равно ускоренно.
22.Момент импульса
Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Моментом импульса L материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r этой материальной точки, проведенного из точки О, на величину ее импульса Р(рис. 6):
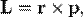 (Дж•с),
(Дж•с),
где 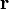 – радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
– радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, 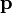 – импульс частицы.
– импульс частицы.
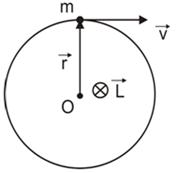
Рис.6.
Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела Lz относительно этой оси (Lz – скалярная величина).
Суммирование производим по всем элементарным массам mi(имеющим линейную скорость vi и радиус вращения ri), на которые разбивается тело. Так как vi=ωri, где ω - угловая скорость вращения тела, а I=∑miri2 - момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен:
Lz = ∑ mi vi ri = ∑ ω mi ri2 = ω ∑ mi ri2 = Iz ω .
В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:
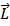 = I
= I 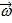 .(1)
.(1)
Продифференцируем выражение (1) по времени:
dLz / dt = Iz dω / dt = Iz e = Mz,
В итоге:
Lz / dt = dMz (2)
Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси:
dL/ dt = M (3)
Из уравнения (3) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.
Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)
Выражение (4) представляет собой закон сохранения момента импульса:
момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.
Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.
Дата добавления: 2017-05-18; просмотров: 2081;
