Применение законов сохранения к столкновению упругих и неупругих тел.
При соударении тела деформируются. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел.
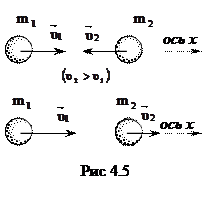 Столкновения могут быть упругими и неупругими. Их предельные идеализированные случаи – абсолютно упругий и абсолютно неупругий удар.
Столкновения могут быть упругими и неупругими. Их предельные идеализированные случаи – абсолютно упругий и абсолютно неупругий удар.
При абсолютно упругом ударе (например, столкновении шаров из слоновой кости или закаленной стали) механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия тел полностью или частично переходит в потенциальную энергию упругой деформации. По завершении удара первоначальная форма тел полностью восстанавливается. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, величина и направление которых определяются законом сохранения механической энергии и законом сохранения полного импульса системы тел.
Пpи неупругом ударе (например столкновении шаров из воска, двух разноименных ионов с образованием молекулы, захвате свободного электрона положительным ионом и т.д.) тела не восстанавливают свою первоначальную форму, кинетическая энергия тел частично или полностью превращается во внутреннюю энергию. При абсолютно неупругом ударе тела движутся после удара как единое целое с одинаковой скоростью или покоятся. При абсолютно неупругом ударе закон сохранения механической энергии не соблюдается. Выполняется лишь закон сохранения импульса и закон сохранения суммарной энергии различных видов – механической и внутренней.
Рассмотрим случай центрального соударения двух однородных шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, соединяющей их центры (рис 4.12).
Поскольку удар упругий, то механическая энергия не переходит в другие виды энергии а кинетическая энергия сохраняется:
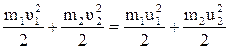 , (4.9)
, (4.9)
где 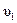 ,
, 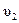 ,
, 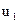 ,
, 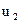 – скорости шаров до и после удара.
– скорости шаров до и после удара.
Потенциальная энергия при упругом столкновении шаров не меняется закон сохранения импульса:
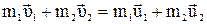 , (4.10)
, (4.10)
Уравнения (4.9) следует:
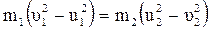 ,
,
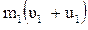
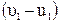 =
=
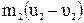
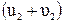 . (4.11)
. (4.11)
Из уравнения (4.10) с учетом проекции скоростей на ось Х:
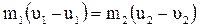 . (4.12)
. (4.12)
Поделив левые и правые части уравнении (4.11) 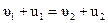 (4.12), получим:
(4.12), получим:
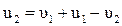
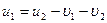 (4.13)
(4.13)
Подставим (4.13) в (4.12):
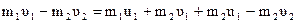 ,
,
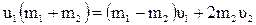 .
.
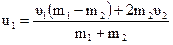 . (4.14)
. (4.14)
По аналогии, подставим в формулу (4.13) полученное значение для 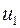 :
:
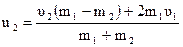 . (4.15)
. (4.15)
Рассмотрим частные случаи.
1) Массы шаров равны 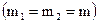 .
.
Дата добавления: 2017-05-18; просмотров: 4197;
