Причина деформации — это движение.

Сила упругости — это сила, которая возникает при упругих деформациях и действует только в процессе деформации.

Закон Гука: сила упругости, которая возникает при упругой деформации, прямо пропорциональна деформации тела, взятой со знаком «минус», и записывается формулой: 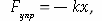, где k — жесткость тела или коэффициент упругости.

Коэффициент жесткости — это физическая величина, которая является характеристикой свойств упругих тел.

Жесткость тела, имеющего цилиндрическую форму, определяется формулой: 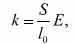характеристикой упругих свойств тела.

Силы трения.
Силы трения — это такие силы, которые возникнут при соприкосновении тел, действующие вдоль соприкасающихся поверхностей, препятствующие их относительному перемещению.
Виды трения:

1. cухое трение:

o трение покоя;

o трение скольжения;

o трение качения.

2. жидкое (вязкое) трение.

Сухое трение — это трение, возникающее между поверхностями двух твердых тел.

Трение покоя — это трение, возникающее при отсутствии относительного движения соприкасающихся поверхностей.

Формула для вычисления силы трения покоя:

Трение скольжения — это трение, возникающее в процессе скольжения одной поверхности по другой.
Трение качения — это трение, возникающее между опорой и катящимся по ней телом.
Сила трения качения — это сила, которая необходима для равномерного прямолинейного качения тела по горизонтальной плоскости.

Закон Кулона: модуль силы трения качения пропорционален коэффициенту трения качения, модулю силы реакции опоры и обратно пропорционален радиусу катящегося тела, и записывается формулой: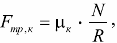

Момент трения — это физическая величина, которую создает пара сил, приложенных к катящемуся телу: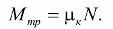

Жидкое (вязкое) трение — это трение, возникающее между поверхностью твердого тела и жидкой (газообразной) средой, где движется твердое тело.

Гравитационное взаимодействие — это самое слабое взаимодействие, которое характеризуется своей универсальностью, это взаимодействие присуще всем материальным объектам.

Гравитационная масса — это физическая величина, которая характеризует способность тела участвовать в гравитационном взаимодействии; эта характеристика определяет гравитационные свойства.

Закон всемирного тяготения: две материальные частицы или материальные точки притягиваются друг к другу с силой, которая определяется отношением их масс к квадрату расстояния между ними

Гравитационная постоянная— это коэффициент пропорциональности, который имеет следующее значение: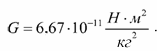

Физический смысл гравитационной постоянной: гравитационная постоянная представляет численное значение силы, с которой притягиваются два тела друг к другу, с массами равными по 1 кг, расположенными на расстоянии 1 м друг от друга.

Формула для гравитационного взаимодействия тела с Землей: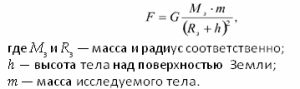

Гравитационное поле (поле тяготения) — это поле, где осуществляется тяготение между телами, гравитационное поле является одной из форм материи.

11.Энергия — универсальная мера различных форм движения и взаимодействия. С раз­личными формами движения материи связывают различные формы энергии: механи­ческую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движе­ния материи не изменяется (например, горячее тело нагревает холодное), в дру­гих — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом.Кинетическая энергия механической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.E_k=mv²/2/

Потенциальная энергия — механическая энергия системы тел, определяемая их вза­имным расположением и

характером сил взаимодействия между ними. Потенциальная энергия тела 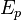в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

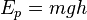
где 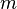— масса тела, 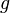— ускорение свободного падения, 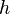— высота положения центра масс тела над произвольно выбранным нулевым уровнем.

Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, —консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипатнвной; ее примером является сила трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении кон­фигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

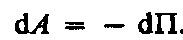
16) Работа. Механическая работа

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы

В механике можно ввести понятие работы, исходя из довольно простых представлений

12.

лучае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 15.1):

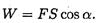
Единицы измерения работы: 1 Дж (джоуль)= 1 Н-м; 1 кДж (килоджоуль) = 103 Дж.

Рассмотрим частные случаи.

1. Силы, совпадающие с направлением перемещения, называ­ются движущими силами.

Направление вектора силы совпадает с направлением перемещения (рис. 15.2). В этом случае α = 0° (cos α = 1). Тогда W = FS > 0.

2. Силы, перпендикулярные направлению перемещения, работы не производят (рис. 15.3).

Сила F перпендикулярна направлению перемещения, α = 90° (cos α = 0); W = 0.

3. Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления (рис. 15.4).

Сила F направлена в обратную от перемещения S сторону. В этом случае α = 180° (cos α = — 1), следовательно, W = — FS < 0.

Движущие силы увеличивают модуль скорости, силы сопротивления уменьшают скорость.

Таким образом, работа может быть положительной и отрица­тельной в зависимости от направления силы и скорости.

13. Пусть тело движется под действием некоторой переменной силы F по прямой, причем направление силы совпадает с направлением движения, а работа А, произведенная силой F при перемещении тела из т.х=а по прямой ОХ в точку х=b той же прямой, может быть выражена (в случае когда F=F(x) есть непрерывная функции на [a; b]) с помощью определенного интеграла следующим образом:

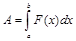. (1)

Пример 13. Рессора прогибается под нагрузкой 1,5 т на 1 см. Какую работу надо затратить для деформации рессора на 3 см? (Сила деформации пропорциональна величине деформации).

Решение: обозначим через х – величину деформации, т.к. F=kx, где k - коэффициент пропорциональности (коэффициент жесткости).

Известно, что при х=0,01 м F=1,500 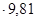(Н),

то 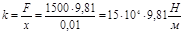, следовательно, .

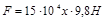По формуле (1) работа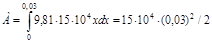

14.

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения^[1].Простым языком, кинетическая энергия - это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю. Работа и изменение скорости тела. Установим связь между работой постоянной силы и изменением скорости тела. В этом случае работу силы можно определить как 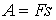. Модуль силы по второму закону Ньютона равен 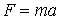, а модуль перемещения 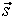при равноускоренном прямолинейном движении

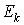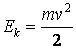: . (19.2)

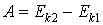. (19.3)Работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела. Это утверждение называют теоремой о кинетической энергии.

Так как изменение кинетической энергии равно работе силы (19.3), кинетическая энергия выражается в тех же единицах, что и работа, т.е. в джоулях.

Если начальная скорость движения тела массой 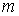равна нулю и тело увеличивает свою скорость до значения 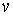, то работа силы равна конечному значению кинетической энергии тела:

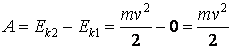. (19.4)Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

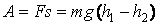. (20.1)что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.При движении вниз работа силы тяжести положительна, при движении вверх - отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т.е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

16.Растворы, осмотическое давление. Влажность: относительная и абсолютная влажность, точка росы.Осмотическое давление(обозначается π) — избыточное гидростатическое давление на раствор, отделённый от чистого растворителя полупроницаемой мембраной, при котором прекращается диффузия растворителя через мембрану (осмос). Это давление стремится уравнять концентрации обоих растворов вследствие встречной диффузии молекул растворённого вещества и растворителя. Величина осмотического давления, создаваемая раствором, зависит от количества, а не от химической природы растворенных в нём веществ (илиионов, если молекулы вещества диссоциируют), следовательно, осмотическое давление является коллигативным свойством раствора. Чем больше концентрация вещества в растворе, тем больше создаваемое им осмотическое давление. Это правило, носящее название закона осмотического давления, выражается простой формулой, очень похожей на некий закон идеального газа: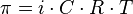,где i — изотонический коэффициент раствора; C — молярная концентрация раствора, выраженная через комбинацию основных единиц СИ, то есть, в моль/м³, а не в привычных моль/л; R — универсальная газовая постоянная; T — термодинамическая температура раствора. Абсолютная влажность воздуха(f)— это количество водяного пара, фактически содержащегося в 1м³воздуха:f= m (масса содержащегося в воздухе водяного пара)/ V (объём влажного воздуха). Обычно используемая единица абсолютной влажности:(f)= г/ Относительная влажность: φ = (абсолютная влажность)/(максимальная влажность). Относительная влажность обычно выражается в процентах. Эти величины связаны между собой следующим отношением: φ = (f×100)/fmax. Точка росы — это температура, до которой должен охладиться воздух, чтобы содержащийся в нём пар достиг состояния насыщения и начал конденсироваться в росу.

17.Кристаллические и аморфные твердые тела. Жидкие кристаллы. Деформация твердых тел. Виды деформации.Твердое тело— агрегатное состояние вещества, характеризующееся постоянством формы и характером движения атомов, которые совершают малые колебания около положений равно­весия. Кристаллические тела. Твердое тело в обычных условиях трудно сжать или растянуть. Для придания твердым телам нужной формы или объема на заводах и фабриках их обрабатывают на специальных станках: токарных, строгальных, шлифовальных. Аморфные тела. Кроме кристаллических, к твердым телам относят также аморфные тела. АТ — это твердые тела, для которых характерно неупорядоченное расположение частиц в пространстве. К аморфным телам относятся стекло, янтарь, различные другие смолы, пластмассы. Хотя при комнатной температуре эти тела сохраняют свою форму, но при повышении температуры они постепенно размягчаются и начинают течь, как жидкости: у аморфных тел нет определенной температуры, плавления. Жидкие кристаллы - Это фазовое состояние, в которое переходят некоторые вещества при определенных условиях (температура, давление, концентрация в растворе). ЖК обладают одновременно свойствами как жидкостей (текучесть), так и кристаллов (анизотропия).Деформация твердого тела-Изменение линейных размеров или форм твердого тела под действием внешних сил. Виды деформаций: Деформация растяжения или сжатия - изменение любого линейного размера тела (длины, ширины или высоты). Деформация сдвига - перемещение всех слоев твердого тела в одном направлении параллельно некоторой плоскости сдвига. Деформация изгиба - сжатие одних частей тела при растяжении других. Деформация кручения - поворот параллельных сечений образца вокруг некоторой оси под действием внешней силы.

18.Механические свойства твердых тел. Закон Гука. Кривая деформации. Пределы упругости и прочности. Пластическая деформация.Под действием приложенных внешних сил твердые тела изменяют свою форму и объем - деформируются. Если после прекращения действия силы, форма и объем тела полностью восстанавливаются, то деформацию называют упругой, а тело - абсолютно упругим. Деформации, которые не исчезают после прекращения действия сил, называются пластическими, а тела - пластичными.Различают следующие виды деформаций: растяжение, сжатие, сдвиг, кручение и изгиб.Деформацию растяжения характеризуют абсолютным удлинением дельта l и относительным удлинением е: 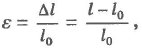где l₀- начальная длина, l- конечная длина стержня. Механическим напряжением называют отношение модуля силы упругости F к площади поперечного сечения тела S:б=F/S.

В СИ за единицу механического напряжения принимают 1Па = 1Н/м².Закон Гука: при малых деформациях напряжение прямо пропорционально относительному удлинению (б = Е • е). Упругой деформацией называется такая, при которой после прекращения действия силы тело восстанавливает свои первоначальные форму и размеры. Пластической деформацией назыв. такая, при которой после прекращения действия нагрузки тело не восстанавливает своей первоначальной формы и размеров. Пластической деформации всегда предшествует упругая.

20.Основное уравнение молекулярно-кинетической теории газов. Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. В модели идеального газа предполагается следующее: молекулы обладают пренебрежимо малым объемом по сравнению с объемом сосуда, между молекулами не действуют силы притяжения, при соударениях молекул друг с другом и со стенками сосуда действуют силы отталкивания. Давление идеального газа. Одним из первых и важных успехов молекулярно-кинетической теории было качественное и количественное объяснение явления давления газа на стенки сосуда. Качественное объяснение давления со стенками сосуда взаимодействуют с ними по законам механики как упругие тела. При столкновении молекулы со стенкой сосуда проекция 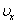вектора скорости на ось ОХ, перпендикулярную стенке, изменяет свой знак на противоположный, но остается постоянной по модулю

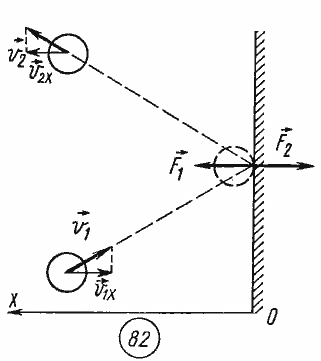
Поэтому в результате столкновения молекулы со стенкой проекция ее импульса на ось ОХ изменяется от 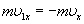до 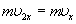. Изменение импульса молекулы показывает, что на нее при столкновении действует сила 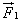, направленная от стенки. Изменение импульса молекулы равно импульсу силы 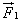: 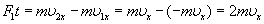Во время столкновения молекула действует на стенку с силой 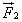, равной по третьему закону Ньютона силе 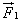по модулю и направленной противоположно. Молекул газа очень много, и удары их о стенку следуют один за другим с очень большой частотой. Среднее значение геометрической суммы сил, действующих со стороны отдельных молекул при их столкновениях со стенкой сосуда, и является силой давления газа. Давление газа равно отношению модуля силы давления 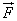к площади стенки S: 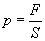На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяло вычислить давление газа, если известны масса m0 молекулы газа, среднее значение квадрата скорости молекул 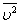и концентрация n молекул: 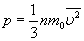-это уравнение называют основным уравнением молекулярно-кинетической теории. Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа 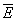: 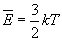получим 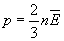. Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

21.Внутренняя энергия системы как функция состояния. Эквивалентность теплоты и работы. Первое начало термодинамики. Внутренняя энергия - термодинамическая функция состояния системы, ее энергия, определяемая внутренним состоянием. Она складывается в основном из кинетической энергии движения частиц (атомов, молекул, ионов, электронов) и энергии взаимодействия между ними (внутри- и межмолекулярной). На внутреннюю энергию влияет изменение внутреннего состояния системы под действием внешнего поля; во внутреннюю энергию входит, в частности, энергия, связанная с поляризацией диэлектрика во внешнем электрическом поле и намагничиванием парамагнетика во внешнем магнитном поле. Кинетическая энергия системы как целого и потенциальная энергия, обусловленная пространственным расположением системы, во внутреннюю энергию не включаются. В термодинамике определяется лишь изменение внутренней энергии в различных процессах. Поэтому внутреннюю энергию задают с точностью до некоторого постоянного слагаемого, зависящего от энергии, принятой за нуль отсчета. Внутренняя энергия U как функция состояния вводится первым началом термодинамики, согласно которому разность между теплотой Q, переданной системе, и работой W, совершаемой системой, зависит только от начального и конечного состояний системы и не зависит от пути перехода, т.е. представляет изменение функции состояния ΔU 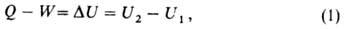где U₁ и U₂ - внутренняя энергия системы в начальном и конечном состояниях соответственно. Уравнение (1) выражает закон сохранения энергии в применении к термодинамическим процессам, т.е. процессам, в которых происходит передача теплоты. Для циклического процесса, возвращающего систему в начальное состояние, ΔU=0. В изохорных процессах, т.е. процессах при постоянном объеме, система не совершает работы за счет расширения, W=0 и теплота, переданная системе, равна приращению внутренней энергии: Q_v=ΔU. Для адиабатических процессов, когда Q=0, ΔU=-W. Внутренняя энергия системы как функция ее энтропии S, объема V и числа молей m_i i-того компонента представляет собой термодинамический потенциал. Это является следствием первого и второго начал термодинамики и выражается соотношением: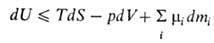

относительная диэлектрическая проницаемость. Электрическая постоянная. Напряженность электрического поля. Диэлектри́ческая проница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая зависимость электрической индукции от напряжённости электрического поля. Относительная диэлектрическая проницаемость ε является безразмерной и показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Эта величина для воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постоянная воды в статическом поле достаточно высока — около 80. Электрическая постоянная (e₀) -физ постоянная, входящая в ур-ния законов электрич. поля (напр., в Кулона закон )при записи этих ур-ний в рационализованной форме, в соответствии с к-рой образованы электрич. и магн. единицы Международной системы единиц; по старой терминологии Э. п. называется диэлектрич. проницаемостью вакуума. 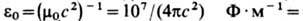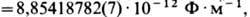где m₀ - магнитная постоянная. В отличие от диэлектрич. проницаемости e, зависящей от типа вещества, темп-ры, давления и др. параметров, Э. п. e₀ зависит только от выбора системы единиц. Напр., в гауссовой СГС системе единиц 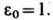напряженность электрического поля в классической электродинамике (E) - векторная характеристика электрич. поля, сила, действующая па покоящийся в данной системе отсчёта единичный олектрич. заряд. При этом предполагается, что внесение заряда (заряженного пробного тела) во внеш. поле E не изменяет такового. Иногда вместо H. э. п. говорят просто "электрич. поле". Размерность Н. э. п. в гауссовой системе - L^-1/2M^1/2T ^-1, в СИ - LMT^-3I^-1; единицей H. э. п. в СИ является вольт на метр (1 СГСЭ = 3^.10⁴ В/м). Распределение H. э. п. в пространстве обычно характеризуют с помощью семейства линий E (силовых линий электрич. поля), касательные к к-рьш в каждой точке совпадают с направлениями вектора E. Как и любое векторное поле, поле E разбивается на две составляющие: потенциальную ([ 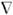E _п) = 0, E _п = - 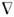j ^е )и вихревую ( 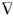Е_B = 0, Е_B = [ 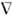A^m]). В частности, электрич. поле, создаваемое системой неподвижных зарядов, является чисто потенциальным. Электрич. поле излучения, в т. ч. поле E в поперечных эл.-магп. волнах, является чисто вихревым. Вместе с вектором магн. индукции В H. э. п. составляет единый 4-тензор электромагнитного поля. Поэтому чисто олектрич. поле данной системы зарядов существует лишь в "избранной" системе отсчёта, где заряды неподвижны. В др. инерцпальных системах отсчёта, перемещающихся относительно "избранной" с пост. скоростью u, возникает ещё имагнитное поле В' = = [uE]/ 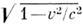, обусловленное появлением конвекц. токов j = ru/ 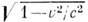(r - плотность заряда в "избранной" системе).

15. Материя — объективная реальность, данная нам В ОЩУЩЕНИЯХ….

Материя несотворима, неуничтожима, вечна и бесконечна.

Типы материальных систем, известные современной науке:

1) элементарные частицы

2) поля

3) атомы

4) молекулы

5) макроскопические тела

6) геологические системы

7) и т.д.

Этим и другим материальным системам соответствуют структурные уровни организации материи (материя структурирована и систематизирована)

Атрибут — неотъемлемое свойство материи.

1) Структурность материи проявляется в су­ществовании бесконечно многообразных материальных образований, каждое из которых представляет собой специфические единичные вещь, процесс, ко­торые локализованы в пространстве и времени: Вселенная, галактика, звезда, планета, молекула, атом, элементарная частица и др. Вместе с тем они тесно взаимосвязаны между собой, так как одни материальные образования явля­ются составными частями других, то есть входят в их структуру в качестве эле­ментов.

2) Системность материи появляется во взаимосвязи вещей и процессов, в регулярном пересечении структурных уровней организации материального мира, в постоянном нарушении автономии, «параллелизма» микро- , макро- и мегамиров, живого и неживого. Основная проблема здесь заключается в не­решенности вопроса перехода от неживой природы к живой в едином эволю­ционном процессе.

Материя— это все то, что прямо или косвенно действует на органы чувств человека и другие объекты. Окружающий нас мир, все существующее вокруг нас представляет собой материю. Неотъемлемое свойство материи — движение.

Движение материи — любые изменения, происходящие с материальными объектами в результате их взаимодействия.

Материя не существует в бесформенном состоянии, из нее образуется сложная иерархическая система материальных объектов различных масштабов и сложностей.

Для естествоиспытателей представляет интерес не материя или движение вообще, а конкретные виды материи и движения.

В современном естествознании различают 3 вида материи:

1. Вещество — основной вид материи, обладающий массой. К вещественным объектам относятся элементарные частицы, атомы, молекулы, многочисленные образовавшиеся из них материальные объекты. В химии вещества подразделяются на простые (с атомами одного химического элемента) и сложные (химические соединения). свойства вещества зависят от внешних условий и интенсивности взаимодействия атомов и молекул. Это и обуславливает различные агрегатные состояния вещества (твердое, жидкое, газообразное + плазма при сравнительно высокой температуре) переход вещества из одного состояния в другое можно рассмотреть как один из видов движения материи.

2. Физическое поле — особый вид материи, который обеспечивает физическое взаимодействие материальных объектов и систем.

Физические поля:

· Электромагнитное и гравитационное

· Поле ядерных сил

· Волновые (квантовые) поля

Источник физических полей — элементарные частицы. Направление для электромагнитного поля — источник, заряженные частицы

Физические поля, которые создаются частицами переносят взаимодействие между этими частицами с конечной скоростью.

Квантовые теории — взаимодействие обусловлено обменом квантами поля между частицами.

3. Физический вакуум — низшее энергетическое состояние квантового поля. Этот термин введен в квантовой теории поля для объяснения некоторых микропроцессов.

Среднее число частиц (квантов поля) вакууме равно нулю, однако в нем могут рождаться виртуальные частицы, то есть частицы в промежуточном состоянии, существующие короткое время. Виртуальные частицы влияют на физические процессы.

Принято считать, что не только вещество, но и поле и вакуум имеют дискретную структуру. Согласно квантовой теории поле, пространство и время в очень малых масштабах образуют пространственно-временную среду с ячейками. Квантовые ячейки настолько малы (10^-35—10^-33 ), что их можно не учитывать при описании свойств электромагнитных частиц, считая пространство и время непрерывными.

Вещество воспринимается как непрерывная сплошная среда. для анализа и описания свойств такого вещества в большинстве случаев учитывается только его непрерывность. Однако, то же вещество при объяснении тепловых явлений, химических связей, электромагнитных излучений рассматривается как дискретная среда, которая состоит из взаимодействующих между собой атомов и молекул.

Дискретность и непрерывность присущи физическому полю, но при решении многих физических задач принято считать гравитационное, электромагнитное и другие поля непрерывными. Однако в квантовой теории поля предполагается, что физические поля дискретны, следовательно, для одних и тех же видов материи характерна прерывность и непрерывность.

Для классического описания природных явлений достаточно учитывать непрерывные свойства материи, а для характеристики различных микропроцессов — дискретные.

Непрерывность и дискретность — неотъемлемые свойства материи.

16.

Потенциальная энергия системы во внешнем поле.
Предположим, что механическая система, состоящая из n частиц, находится во внешнем потенциальном поле. Определим работу, которую совершают внешние консервативные силы на перемещение механической системы за элементарный промежуток времени.
Как убедились, любая частица в потенциальном поле наделена потенциальной энергией. Обозначим потенциальные энергии частиц механической системы как 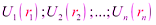, где 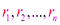радиус-векторы, характеризующие положения частиц.
Покажем, что потенциальная энергия системы во внешнем потенциальном поле есть сумма потенциальных энергий составляющих систему частиц:

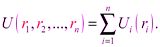
Пусть частицы системы за элементарный промежуток времени dt совершили перемещения 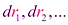. Согласно результату, полученному выше, работа сил поля на перемещение любой частицы равна убыли потенциальной энергии этой частицы:

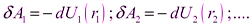
Суммируя эти элементарные работы, получим полную работу внешних консервативных сил на перемещение системы за время dt:
.
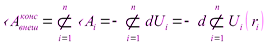Это доказывает утверждение (6.34): работа внешних консервативных сил равна убыли потенциальной энергии системы в силовом поле:

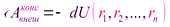
Градиент скалярной функции – это вектор, указывающий направление наиболее быстрого возрастания скалярной функции и по абсолютному значению равный наибольшей скорости возрастания этой функции.

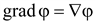
Градиент направлен по нормали к поверхности равного уровня скалярной функции в данной точке. Градиент скалярного потенциала φ постоянного во времени поля равен:

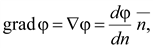
где 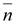– нормаль к эквипотенциальной поверхности в данной точке поля.

Градиент скалярного потенциала φ в каждой точке совпадает с касательной к силовой линии напряженности электрического поля 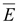в данной точке и имеет направление, противоположное вектору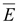

Потенциальная энергия 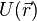— скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в полеконсервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.

Потенциальная энергия тела 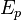в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

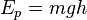
где 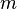— масса тела, 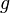— ускорение свободного падения, 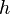— высота положения центра масс тела над произвольно выбранным нулевым уровнем.

17. Если на материальную точку действует сила вида

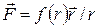, (8)

то говорят, что материальная точка находится в поле центральных сил, если начало координат совпадает с центром сил.

Примерами материальных точек в таком поле являются искусственные спутники Земли.

Очевидно, что момент 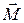центральных сил 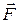относительно центра сил 0 равен нулю. Следовательно, при движении в центральном поле момент импульса материальной точки остается постоянным.

Вектор 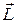всегда ортогонален плоскости векторов 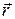и 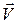. Поэтому постоянство направления 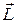свидетельствует о том, что движение материальной точки в поле центральных сил происходит в одной плоскости.

Материальная точка, движущаяся в поле центральных сил, представляет собой консервативную систему. Поэтому при движении материальной точки сохраняется и полная механическая энергия точки, т. е.

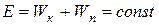. (9)

Для гравитационного центрального поля большой массы М имеем

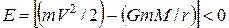. (10)

В этом случае траекторией материальной точки является эллипс, один из фокусов которого совпадает с центром силы, т. е. с положением центра массы М. При E = 0 траекторией частицы является парабола, а при Е > О – гипербола.

18.

Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.

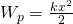
Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.

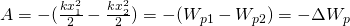
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.

Так же есть:

Потенциальная энергия :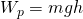

Кинетическая энергия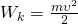

Тут мы использовали :

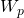— Потенциальная энергия упруго деформированного тела

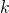— Коэффициент упругости пружины

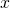— Деформация пружины