Физические основы механики
Механическое движение – это процесс изменения положения данного тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.
Тело, условно принятое за неподвижное – тело отсчета.
Тело отсчета – это тело, относительно которого опре-деляется положение другого тела.
Обычно в качестве тела отсчета выбирается земля, но может быть и движущийся относительно земли предмет: автомобиль, лодка, самолет и т.д.
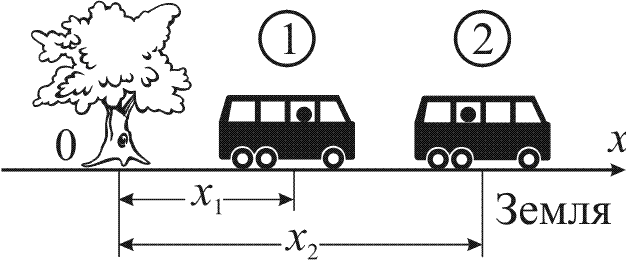
Рис. 1.
Пример. Автомобиль (рис. 1) движется относительно тела отсчета – дерева. Человек вместе с автомобилем движется относительно этого тела отсчета, но относительно другого тела отсчета (автомобиль) находится в покое.
Механическое движение всегда относительное.
Механический покой всегда относительный.
Система отсчета – это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.
Простейшей системой координат является прямоугольная декартова система (рис. 2). Система координат нужна для определения положения тела относительно тела отсчета. Выбор системы отсчета зависит от условий дан-ной задачи.
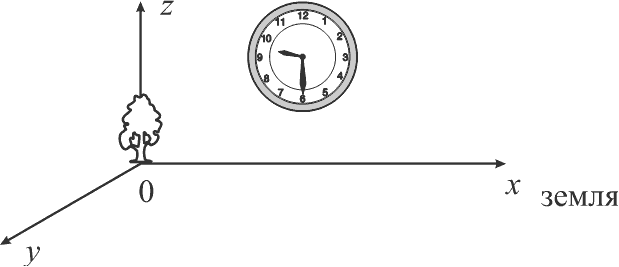
Рис. 2.
Движение реальных тел, как правило, сложное. Для упрощения рас-смотрения движений пользуются моделями. Одними из первых моделей реальных тел являются абсолютное твердое тело и материальная точка.
Абсолютно твердым телом называется тело, рас-стояние между любыми двумя точками которого остается постоянным при любых внешних воздействиях.
Эта модель позволяет исключить деформацию тел при движении. Изу-чив движение абсолютно твердого тела, мы понимаем закономерности движения реальных твердых тел.
Простейшими видами механического движения абсолютно твердого тела являются поступательное (рис. 3) и вращательное (рис. 4).
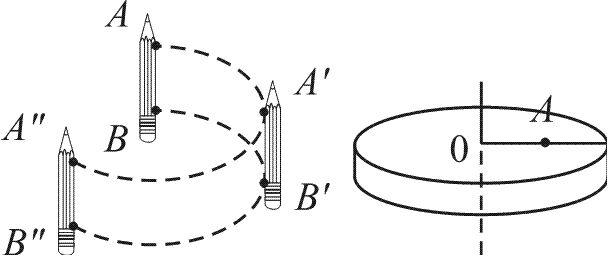
Рис. 3
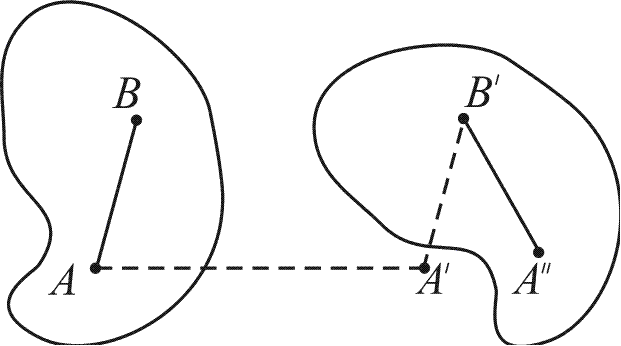
Рис. 4
Поступательным движением называется движение, при котором любая прямая, соединяющая две произ-вольные точки тела, перемещается параллельно самой себе. При поступательном движении траектории всех точек тела одинаковы. Таким образом, для описания поступательного движения тела достаточно описать движение какой-либо одной его точки (т.е. рассмотреть кинематику прямолинейного движения материальной точки).
Вращательным движением называется такое движе-ние, при котором все точки тела описывают окружности в параллельных плоскостях, а центры этих окружностей лежат на одной прямой, называемой осью вращения (неподвижная ось – рис. 3). Любое плоское движение можно представить как результат поступательного движения вдоль ВВ' и «чистого вращения» на угол А'В'А'' – рис. 4. Изучая характер движения Земли, планет относительно Солнца, мы можем не учитывать размеры этих тел и считать их материальными точками (т.е. рассмотреть кинематику криволинейного движения материальной точки).
Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. Данное понятие является математической абстракцией. Одно и то же тело в одних задачах можно рассматривать как материальную точку, а в других задачах – нельзя. Например, радиус Земли RЗемли равен 6400 км, расстояние между Солнцем и Землей L равно 150 000 000 км (L >> RЗемли). Рассматривая движение Земли относительно Солнца, радиусом Земли можно пре-небречь и считать, что Земля – материальная точка. Однако если нужно выяснить причины смены времен года, то Землю уже нельзя считать матери-альной точкой, а надо учитывать ее размеры, вращение вокруг оси и т.д. Мы будем изучать механическое движение материальной точки для того, чтобы потом определить движение реального тела.
Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью. Такое движение называется прямолинейнымравномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроецировать на ось OX и рассматривать их проекции как алгебраические величины.
Прямолинейное равномерное движение,  ,
, 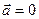 :
:
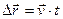 ,
, 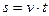 ,
, 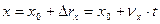 , (2.9)
, (2.9)
где 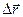 - перемещение;
- перемещение; 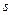 - пройденный путь;
- пройденный путь; 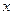 - координата в момент времени t;
- координата в момент времени t; 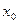 - координата в начальный момент времени t=0. Зависимость координаты x от времени t линейная, график зависимости x(t) представляет собой прямую линию.
- координата в начальный момент времени t=0. Зависимость координаты x от времени t линейная, график зависимости x(t) представляет собой прямую линию.
Прямолинейное равнопеременное движение,  :
:
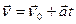 ,
, 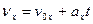 , (2.10)
, (2.10)
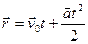 ,
, 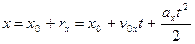 , (2.11)
, (2.11)
где х – координата движущейся точки в момент времени t; x0 – координата в момент времени 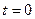 ;
; 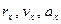 - проекции соответствующих векторов на ось х.
- проекции соответствующих векторов на ось х.
При использовании путевого способа описания движения зависимость пройденного пути s и зависимость величины скорости v от времени будут иметь вид:
 ,
, 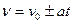 . (2.12)
. (2.12)
Следует помнить, что этими уравнениями можно пользоваться при условии, что при равнозамедленном движении (в формулах ставятся знаки «минус») направление движения на заданном промежутке времени не меняется.
Зависимость проекции скорости 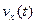 от времени является линейной, график зависимости имеет вид прямой линии. По наклону графика скорости может быть определена проекция ускорения aх .
от времени является линейной, график зависимости имеет вид прямой линии. По наклону графика скорости может быть определена проекция ускорения aх .
Зависимость координаты x(t) от времени является квадратичной, график зависимости является параболой. Вершина параболы соответствует моменту времени, когда направление движения меняется на противоположное. Зависимость пути  от времени тоже является квадратичной, но только с течением времени пройденный путь всегда возрастает.
от времени тоже является квадратичной, но только с течением времени пройденный путь всегда возрастает.
Понятия скорости и ускорения естественным образом обобщаются на случай движения материальной точки по криволинейной траектории. Положение движущейся точки на траектории задается радиус-вектором r, проведенным в эту точку из какой-либо неподвижной точки О, например, начала координат (рис. 1.2). Пусть в момент времени t материальная точка находится в положении М с радиус-вектором r = r(t). Спустя короткое время Dt, она переместится в положение М1 с радиусом – вектором r1=r(t+Dt). Радиус – вектор материальной точки получит приращение, определяемое геометрической разностью Dr=r1-r. Средней скоростью движения за время Dt называется величина
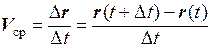 . (1.8)
. (1.8)
Направление средней скорости Vср совпадает с направлением вектора Dr.
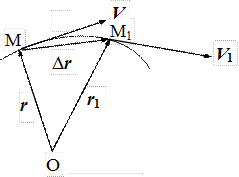
Рис. 1.2
Предел средней скорости при Dt ® 0, т. е. производная радиуса – вектора r по времени
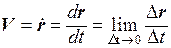 (1.9)
(1.9)
называется истинной или мгновенной скоростью материальной точки. Вектор V направлен по касательной к траектории движущейся точки.
Ускорением а называется вектор, равный первой производной вектора скорости V или второй производной радиуса – вектора r по времени:
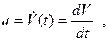 (1.10)
(1.10)
 (1.11)
(1.11)
Отметим следующую формальную аналогию между скоростью и ускорением. Из произвольной неподвижной точки О1 будем откладывать вектор скорости V движущейся точки во всевозможные моменты времени (рис. 1.3).
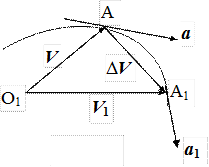
Рис. 1.3.
Конец вектора V называется скоростной точкой. Геометрическое место скоростных точек есть кривая, называемая годографом скорости. Когда материальная точка описывает траекторию, соответствующая ей скоростная точка движется по годографу.
Рис. 1.2 отличается от рис. 1.3 только обозначениями. Радиус – вектор r заменен на вектор скорости V, материальная точка – на скоростную точку, траектория – на годограф. Математические операции над вектором r при нахождении скорости и над вектором V при нахождении ускорения совершенно тождественны.
Скорость V направлена по касательной траектории. Поэтому ускорение a будет направлено по касательной к годографу скорости. Можно сказать, что ускорение есть скорость движения скоростной точки по годографу. Следовательно, все соотношения и теоремы, полученные для скорости, остаются справедливыми и для ускорения, если в них произвести замену величин и терменов согласно следующей таблице:
| Материальная точка Радиус – вектор Траектория Скорость | ® ® ® ® | Скоростная точка Вектор скорости Годограф Ускорение |
В качестве простейшего примера найдем ускорения точки, равномерно вращающейся по окружности радиуса r (Рис.1.4.а). Скорость V направлена по касательной к окружности, ее величина определяется выражением 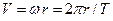 . Годоргафом будет окружность радиуса V (Рис.1.4.б). Когда материальная точка М вращается по окружности радиуса r, соответствующая ей скоростная точка А вращается в том же направлении по окружности радиуса V, описывая эту окружность за то же время Т. Положениям материальной точки на траектории М1, М2, М3, М4 соответствуют на годографе положения скоростной точки А1, А2, А3, А4 . Ускорение а направлено по касательной к окружности – годографу и притом к центру О траектории вращающейся точки М. По аналогии с формулой
. Годоргафом будет окружность радиуса V (Рис.1.4.б). Когда материальная точка М вращается по окружности радиуса r, соответствующая ей скоростная точка А вращается в том же направлении по окружности радиуса V, описывая эту окружность за то же время Т. Положениям материальной точки на траектории М1, М2, М3, М4 соответствуют на годографе положения скоростной точки А1, А2, А3, А4 . Ускорение а направлено по касательной к окружности – годографу и притом к центру О траектории вращающейся точки М. По аналогии с формулой 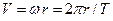 , для величины ускорения можно написать
, для величины ускорения можно написать
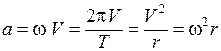 . (1.12)
. (1.12)

а) б)
Рис. 1.4
(1.12) есть центростремительное ускорение. Ее можно записать в векторной форме
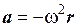 . (1.13)
. (1.13)
Знак минус указывает на то, что направления векторов а и r взаимно противоположны, т.е. ускорение а направлено к центру круговой траектории, по которой вращается материальная точка. Можно также написать для любого положения движущейся точки
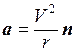 , (1.14)
, (1.14)
где n – единичный вектор нормали к круговой траектории движущейся точки, направленный к центру О (см. рис.1.4а).
Имея в виду дальнейшие обобщения, представим вектор скорости в виде V= Vt, где t- единичный вектор касательной к окружности. Первый множитель V дает численную величину скорости, второй множитель t указывает ее направление. При равномерном вращении абсолютное значение скорости V остается неизменным, меняется только направление скорости, т. е. единичный вектор t. Дифференцированию подлежит только этот вектор, а потому 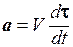 . Сравнивая это выражение с (1.14), получим
. Сравнивая это выражение с (1.14), получим
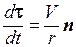 . (1.15)
. (1.15)
Формулу (1.15) можно использовать в случе произвольной гладкой кривой. Здесь необходимо ввести два новых понятия: величина 1/r и единичный вектор n. Величина 1/r называется кривизной кривой, r – радиусом кривизны, а n – единичным вектором главной нормали к кривой. При этом кривизна 1/r считается существенно положительной. А потому единичный вектор n всегда направлен сторону вогнутости кривой.
Рассмотрим общий случай движения материальной точки по криволинейной траектории. Запишем вектор скорости в виде V = Vt. Продифференцировав правую и левую часть по времени, получим
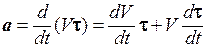 , (1.16)
, (1.16)
или, с учетом формулы (1.15),
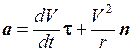 . (1.17)
. (1.17)
Ускорение а направлено под углом к траектории. Первое слагаемое в формуле (1.17)
 (1.18)
(1.18)
есть вектор, направленный по касательной к траектории. Этот вектор называется касательным или тангенциальным ускорением. Второе слагаемое
 (1.19)
(1.19)
есть вектор, направленный вдоль главной нормали в сторону вогнутости траектории. Он называется нормальным ускорением. Таким образом, в общем случае ускорение аможно представить в виде геометрической суммы тангенциального и нормального ускорения:
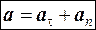 . (1.20)
. (1.20)
Тангенциальное ускорение меняет скорость только по величине, нормальное ускорение меняет ее только по направлению.
Модуль полного ускорения точки
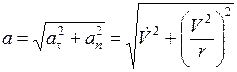 . (1.21)
. (1.21)
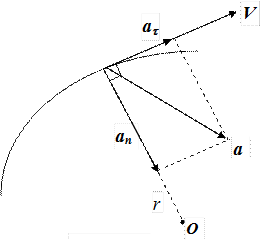
Рис. 1.5
Направления полного ускорения и его составляющих (аt, аn) для случая ускоренного движения приведены на рис. 1.5. При замедленном движении вектор аt имеет противоположноенаправление.
Характеристика движения материальной точки в зависимости
от тангенциальной и нормальной составляющих ускорения
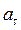
| 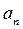
| Движение |
| Прямолинейное равномерное | ||
| const | Прямолинейное равнопеременное | |
| const | Равномерное по окружности | |
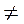 0 0
| Равномерное криволинейное | |
| const | 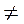 0 0
| Криволинейное равнопеременное |
Табл. 1.1
Поступательное движение. Это такое движение тела, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению. Например, вагон, движущийся по прямому участку пути; кабина колеса обозрения и др.
При поступательном движении все точки тела совершают за один и тот же промежуток времени равные перемещения. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Таким образом, поступательное движение тела может быть полностью описано, если известны зависимость от времени радиуса - вектора r (t) любой точки этого тела и положение последнего в начальный момент.
1. Может ли криволинейное движение быть равномерным?
2. Чему равно скалярное произведение скорости и ускорения в случае равномерного движения по окружности?
3. Что характерно для скоростей и ускорений точек тела, движущегося поступательно?
4. В каких случаях модуль перемещения точки равен длине пути, пройденного точкой за тот же промежуток времени?
5. Как движется точка, если скорость этой точки все время ортогональна ее ускорению?
6. Какова траектория плоского движения точки, если ее радиальная скорость равна нулю?
Задачи
1. Можно ли утверждать, что точка движется без ускорения в случаях:
а) u = const; б) u= const?
2. Является ли движение точки обязательно прямолинейным в случаях:
а) u= const; б) a= const?
3. Точка движется равномерно по окружности. Начало ее радиус-вектора r совпадает с центром окружности. Отличны ли от нуля выражения dr/dt и dV/dt?
4. При каком движении материальной точки выполняются соотношения at = 0, an = const ¹ 0: а) при равномерном движении по окружности; б) при равномерном движении по винтовой линии; в) при равномерном прямолинейном движении; г) при равнопеременном движении по окружности?
1) а, б, в; 2) а, б; 3) г; 4) а; 5) а, б, г.
5. Применима ли для вычисления тангенциального ускорения формула at = u/t в случаях: а) u= 2t + 6; б) u = 3t2; в) u = 5t (u– в м/с; t – в с)?
6. Математический маятник совершает гармонические колебания. Отличны ли от нуля в крайней точке траектории маятника:
а) нормальное ускорение; б) тангенциальное ускорение?
7. Тело бросили вертикально с некоторой высоты: а) вверх;
б) вниз. Начальные скорости в обоих случаях одинаковы. Сравнить скорости в момент падения тела на землю. Сопротивлением воздуха пренебречь.
8. Какой график скорости соответствует графику пути на рисунке?

9. Применима ли для вычисления углового ускорения формула e = w/t в случаях: а) w = 2t + 8; б) w = 9t; в) w = 6 (w – в рад/с, t – в с)?
10. Движение тела с неподвижной осью задано уравнением j = 2p(6t – 3t2) (j – в рад, t – в с). Начало движения при t = 0. Сколько оборотов сделает тело до момента изменения направления вращения?
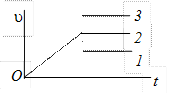
11. Стержень длиной l упирается верхним концом в стену, а нижним – в пол. Конец, упирающийся в стену, равномерно опускается вниз. Будет ли движение другого конца равномерным?
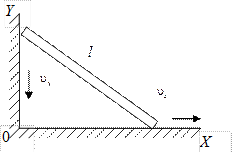
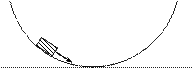
12. У подножия горы санкам сообщена некоторая скорость, в результате чего санки въезжают на гору и, достигнув точки А начинают скользить обратно. Как направлены нормальное и тангенциальное ускорения в точке А.
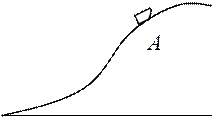
13. Тело скользит без трения по вогнутой поверхности. Как в наинизшей точке направлены нормальное и тангенциальное ускорения.
4. Пусть некоторая точка движется по окружности радиуса r. Изменение положения точки в пространстве за промежуток времени Dt определяется углом поворота 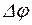 (рис. 3). Элементарный поворот на угол
(рис. 3). Элементарный поворот на угол 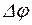 можно рассматривать как вектор
можно рассматривать как вектор 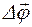 . Модуль вектора
. Модуль вектора 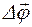 равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняетсяправилу правого винта.
равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняетсяправилу правого винта.
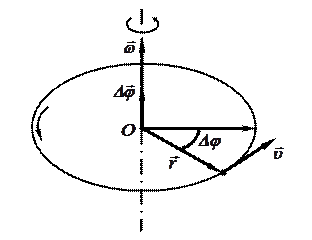
|
Рис. 3
Угловой скоростью 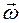 называется векторная величина, равная пределу отношения угла поворота
называется векторная величина, равная пределу отношения угла поворота 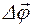 к промежутку времени Dt, за который этот поворот произошел, при стремлении Dt к нулю:
к промежутку времени Dt, за который этот поворот произошел, при стремлении Dt к нулю:
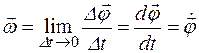 ,
,
где 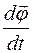 – первая производная от функции угла поворота
– первая производная от функции угла поворота 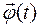 радиус-вектора
радиус-вектора 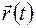 по времениt. Эту производную принято обозначать, как
по времениt. Эту производную принято обозначать, как 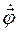 .
.
Вектор 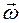 направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
Угловым ускорением 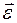 называется векторная величина, равная пределу отношения изменения угловой скорости
называется векторная величина, равная пределу отношения изменения угловой скорости 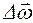 к промежутку времени Dt, за который это изменение произошло, при стремлении Dt к нулю:
к промежутку времени Dt, за который это изменение произошло, при стремлении Dt к нулю:
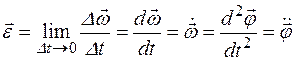 ,
,
где 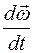 – первая производная от функции
– первая производная от функции 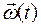 по времениt,
по времениt,
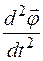 – вторая производная от функции
– вторая производная от функции 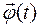 по времениt.
по времениt.
Эти производные принято обозначать соответственно в виде: 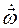 и
и 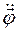 .
.
Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном вращении направление вектора 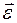 совпадает с направлением вектора угловой скорости
совпадает с направлением вектора угловой скорости 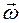 , а при замедленном – противоположно ему.
, а при замедленном – противоположно ему.
Кинематические параметры поступательного и вращательного движения связаны между собой. Связь скорости 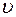 и угловой скорости
и угловой скорости 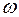 (см. рис. 3) определяется следующим образом:
(см. рис. 3) определяется следующим образом:  .
.
В векторном виде эту связь для векторов 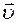 и
и 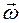 можно записать с помощью векторного произведения:
можно записать с помощью векторного произведения: 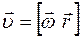 .
.
Ускорение а также можно выразить через угловые параметры, разложив ускорение а на две составляющие 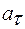 и
и  , то есть:
, то есть: 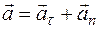 .
.
Тангенциальная составляющая 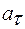 выражается через угловое ускорение
выражается через угловое ускорение 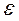 :
:
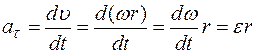 ,
,
а нормальная составляющая  – через угловую скорость
– через угловую скорость 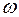 :
:
 .
.
Тогда ускорение: 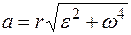 .
.
При равномерном вращении угловая скорость 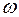 не изменяется. В этом случае вращение можно характеризовать периодом вращенияT , то есть временем, за которое точка совершает один полный оборот.
не изменяется. В этом случае вращение можно характеризовать периодом вращенияT , то есть временем, за которое точка совершает один полный оборот.
Угловая скорость равномерного вращения связана с периодом вращения:
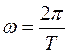 .
.
Частотой вращенияn называется число полных оборотов, совершаемых телом в единицу времени. При равномерном вращении:
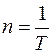 , откуда
, откуда 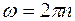 .
.
5. Рассмотрим движение материальной точки по окружности. Положение точки М на окружности можно задать угловой координатой – углом a, который образует радиус – вектор ОМ с каким - либо неизменным направлением, например, с осью ОХ (рис. 1.1).
Производная угловой координаты a по времени
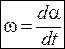 (1.4)
(1.4)
называется угловой скоростью. Вращение называется равномерным, если угловая скорость постоянна, w=const. Величина n = 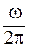 называется частотой обращения. Величина Т =1/n называется периодом вращения.
называется частотой обращения. Величина Т =1/n называется периодом вращения.

Рис. 1.1
Первая производная угловой скорости w по времени или вторая производная угловой координаты 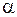 по времени называется угловым ускорением:
по времени называется угловым ускорением:
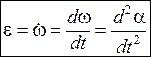 . (1.5)
. (1.5)
Если через S обозначить длину дуги окружности ХМ, то ее производные V = dS/dt и 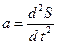 дают линейную скорость и линейное ускорение при движении точки по окружности. Если r – радиус окружности, то S = ra. Дифференцируя это соотношение по времени, находим
дают линейную скорость и линейное ускорение при движении точки по окружности. Если r – радиус окружности, то S = ra. Дифференцируя это соотношение по времени, находим
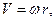 (1.6)
(1.6)
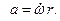 (1.7)
(1.7)
6. Первый закон Ньютона (закон инерции) формулируется следующим образом: всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии или взаимном уравновешивании внешних воздействий называется инертностью. Если на тело действует неуравновешенная система сил, то инертность сказывается в том, что изменение состояния покоя или движения тела происходит постепенно, а не мгновенно. При этом движение изменяется тем медленнее, чем больше инертность тела. Мерой инертности тела при поступательном движении является масса.
Первый закон Ньютона выполняется не во всякой системе отсчета. Системы, в которых он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно, или по инерции. Система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением, является неинерциальной, и в ней не выполняются ни закон инерции, ни второй закон Ньютона, ни закон сохранения импульса.
Понятие «инерциальная система отсчета» является научной абстракцией. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом (Землей, корпусом корабля и т.п.), по отношению к которому и изучается движение тех или иных объектов. Однако в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звездам), поэтому любая реальная система отсчета может рассматриваться как инерциальная лишь с той или иной степенью приближения. С очень высокой степенью точности инерциальной можно считать гелиоцентрическую (звездную) систему с началом координат в центре Солнца и с осями, направленными на три звезды. Для решения большинства технических задач инерциальной системой можно считать систему отсчета, жестко связанную с Землей (не учитывается вращение Земли вокруг собственной оси и вокруг Солнца).
Как уже отмечалось, масса – это физическая величина, определяющая инерционные свойства материи. Масса – это свойство самого тела и, в отличие от веса, не зависит от места ее измерения (вес Р тела в разных точках земного шара различен: он максимален на полюсах и минимален на экваторе). Ускорение свободного падения g тел на Землю также зависит от географической широты места наблюдения и от его высоты над уровнем моря. Однако отношение веса тела Р к его ускорению g одинаково во всех точках земного шара. Это отношение и принято для количественного измерения массы:
 (2.1)
(2.1)
За единицу массы принят килограмм массы, равный массе эталона, сделанного из сплава иридия и платины. Следует отметить, что масса тела считается постоянной величиной только в классической механике Ньютона, изучающей движение тел со скоростями, небольшими по сравнению со скоростью света (  ). В современной физике установлено, что масса тела увеличивается с увеличением скорости его движения по закону:
). В современной физике установлено, что масса тела увеличивается с увеличением скорости его движения по закону:
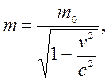
где m – масса тела, движущегося со скоростью 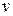 ; с – скорость света; m0 – масса покоящегося тела.
; с – скорость света; m0 – масса покоящегося тела.
Из формулы (2.1) следует, что вес тела
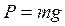 , (2.2)
, (2.2)
т.е. вес – это сила, с которой тело притягивается Землей, т.е. та сила, которая сообщает телу ускорение g=9,81 м/с2:
1 кГ=1 кг·9,81 м/с2 .
С другой стороны,
1 Н=1 кг·1 м/с2 ,
следовательно,
1 кГ=9,81 Н.
Для описания воздействий тел (материальных точек) друг на друга вводится понятие силы. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорения (динамическое проявление сил), либо деформируются, т.е. изменяют свою форму и размеры (статическое проявление сил). Таким образом, сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. В каждый момент времени сила характеризуется числовым значением (модулем), направлением в пространстве и точкой приложения.
Пример. Какого веса балласт Fx надо сбросить с равномерно спускающегося аэростата, чтобы он начал подниматься с той же скоростью? Вес аэростата с балластом Р=1600 кГ, подъемная сила аэростата F1=1200 кГ. Силу сопротивления воздуха F2 считать одинаковой при подъеме и при спуске.
Дата добавления: 2017-05-18; просмотров: 2453;
