Деформации твердых тел подчиняются закону Гука до известного предела. Связь

*С. Пуассон (1781—1840) — французский ученый. ••Т. Юнг (1773—1829) — английский ученый.

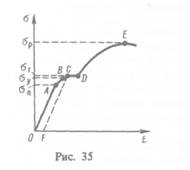
между деформацией и напряжением представляется в виде диаграммы напряжений, качественный ход которой мы рассмотрим для металлического образца (рис. 3S). Из рисунка видно, что линейная зависимость 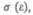установленная Гуком, выполняется

лишь в очень узких пределах до так называемого предела пропорциональности 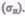При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость 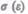уже нелинейна) и до предела упругости 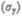остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации и график, описыва­ющий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, а параллельной ей — CF. Напряжение, при котором появляется заметная остаточная деформация 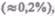называется пределом текучести

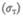— точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести зна­чительна, называются вязкими, для которых же она практически отсутствует — хруп­кими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Мак­симальное напряжение, возникающее в теле до разрушения, называется пределом прочности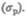

Диаграмма напряжений для реальных твердых тел зависит от различных факторов. Одно и то же твердое тело может при кратковременном действии сил проявлять себя как хрупкое, а при длительных, но слабых силах является текучим.

Вычислим потенциальную энергию упругорастянутого (сжатого) стержня, которая равна работе, совершаемой внешними силами при деформации:

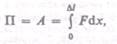
где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до 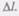Согласно закону Гука (21.4), 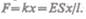Поэтому

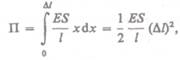
т. е. потенциальная энергия упругорастянутого стержня пропорциональна квадрату деформации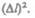

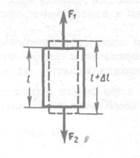
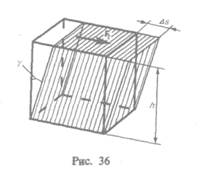
Деформацию сдвига проще всего осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу 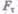(рис. 36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется из формулы

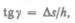
где 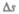— абсолютный сдвиг параллельных слоев тела относительно друг друга; Л — расстояние между слоями (для малых углов ).

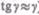Задачи

Глава 5 Тяготение. Элементы теории поля