Уравнение больцмана

Состояние системы можно описать либо указав значения температуры, давления, объема и других свойств – это будет характеристика макросостояния системы, либо, указав свойства каждой частицы вещества, то есть ее положение в пространстве, массу, скорость и направление движения – это будет характеристика микросостояния системы.

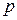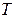Если рассмотреть некоторое количество газа с заданными термодинамическими параметрами , и , то при постоянных внешних условиях макросостояние газа не изменяется, однако молекулы газа находятся в непрерывном хаотическом движении и данному макросостоянию будет отвечать большое число различных микросостояний, которое называется термодинамической вероятностью 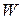. Величина 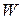– есть мера вероятности данного макросостояния: чем больше 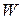, тем вероятнее пребывание системы в данном состоянии.

Процессы в изолированной системе направлены в сторону увеличения ее термодинамической вероятности. Равновесное состояние системы – это наиболее вероятное состояние. Как следует из II закона термодинамики, самопроизвольные процессы в изолированной системе характеризуются увеличением ее энтропии. Поэтому можно предположить, что энтропия и термодинамическая вероятность функционально связаны друг с другом. Связь между энтропией и термодинамической вероятностью выражается уравнением Больцмана:

.

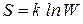Уравнение Больцмана лежит в основе современной статистической термодинамики и позволяет понять свойства энтропии как функции состояния. При абсолютном нуле в системе абсолютный порядок ( 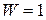) и энтропия 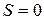. При нагревании системы возникает тепловое движение, беспорядок в системе увеличивается и энтропия возрастает. Энтропия – мера беспорядка в системе.