Реакций и других процессов. уравнение кирхгофа

Температура оказывает большое влияние на тепловые эффекты химических реакций.

Зависимость теплового эффекта химической реакции от температуры выражает закон Кирхгофа:

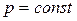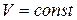Температурный коэффициент теплового эффекта химической реакции (или другого процесса), протекающей при или равен разности теплоемкостей системы в конечном 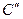и исходном 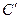состоянии.

Для процесса, протекающего при 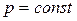закон Кирхгофа выражается уравнением:

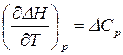, (15)

где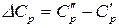

Для химической реакции

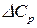равно

.

Аналогично для процессов, протекающих при 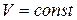, запишем:

.

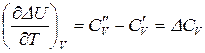Для химической реакции

.

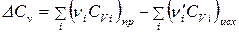Согласно уравнению Кирхгофа (15) влияние температуры на тепловой эффект обусловливается знаком величины 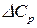. Если 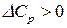, то производная 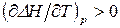, следовательно, с повышением температуры тепловой эффект реакции будет возрастать. Если 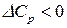, то производная 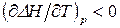, следовательно, с повышением температуры тепловой эффект реакции уменьшается. При 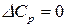тепловой эффект реакции не зависит от температуры.

Закон Кирхгофа позволяет рассчитать тепловые эффекты реакции при различной температуре. Получим уравнение для расчета теплового эффекта, для чего разделим переменные в уравнении (15):

.

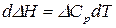При интегрировании уравнения Кирхгофа часто используется температурная зависимость теплоемкости в виде степенных рядов, которые справедливы в определенном интервале температур:

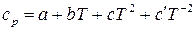. (16)

где а, b, c и 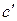– эмпирические коэффициенты, вычисленные на основе экспериментальных данных о 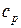, причем коэффициент 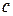относится к органическим веществам, а 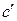– к неорганическим. Значения коэффициентов для различных веществ приведены в справочнике и применимы только для указанного интервала температур.

Чаще всего интегрирование проводят в определенных пределах, приняв за нижний предел интегрирования стандартную температуру 298 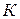, а за верхний температуру 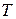. Тепловой эффект реакции при 298 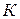легко рассчитать, используя первое или второе следствие из закона Гесса. В результате интегрирования получим:

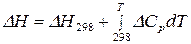. (17)

Так как теплоемкость при 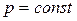обладает свойствами функции состояния, разность 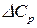рассчитывается:

,

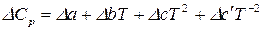где 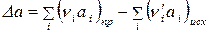; и т.д.

Подставим выражение для 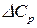в уравнение для теплового эффекта и проведем интегрирование. В результате получим:

(18)

Вычисление теплового эффекта по уравнению Кирхгофа значительно упрощается, если при его интегрировании воспользоваться вместо температурных рядов средними теплоемкостями 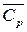для реагентов или принять, что 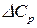не зависит от температуры в данном интервале. После интегрирования получим:

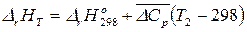, (19)

где .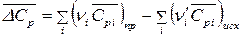

1.4. Второй закон термодинамики

1.4.1. Математическое выражение II закона термодинамики