Внутренняя энергия как функция состояния системы

Физическая химия

Физическая химия – наука о взаимосвязи физических и химических явлений.

Главное внимание в физической химии уделяется исследованию закономерностей протекания химических процессов: определению возможности осуществления, направления, механизма, скорости и конечных результатов при различных условиях. Основная задача физической химии – предсказание пути протекания химического процесса и выхода конечных продуктов, что позволяет управлять процессом, обеспечивать наиболее полное и быстрое его проведение.

1. Химическая термодинамика

Термодинамика – наука о взаимном превращении одних видов энергии в другие.

1.1. Основные понятия и определения

Система – это тело или совокупность тел, мысленно ограниченных от окружающей среды. Система может быть открытой, закрытой или изолированной.

Открытая система способна обмениваться с окружающей средой и веществом и энергией. Например, все открытые реакторы, все явления, протекающие в природе.

Закрытая система может обмениваться с окружающей средой только энергией. Например, закрытые реакторы.

Изолированная система лишена возможности обмениваться с окружающей средой и энергией и веществом. Например, адиабатические реакторы (в технике).

Любая термодинамическая система характеризуется определенным состоянием, которое определяется совокупностью термодинамических параметров состояния. Все параметры состояния подразделяются на две группы:

1) внешние параметры, оказывающие воздействие на всю систему. Например, давление, температура, объем (если система помещена в магнитное поле, то внешним параметром будет являться напряженность магнитного поля и т.д.);

2) внутренние параметры – не зависящие от общего объема или массы системы. Например, концентрации веществ, входящих в систему.

Уравнение, связывающее параметры состояния, называют уравнением состояния термодинамической системы.

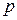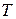Пример: если выбрать в качестве системы какой-либо идеальный газ, то основными параметрами будут являться давление , объем и температура . Уравнение, связывающее параметры состояния идеального газа – уравнение Менделеева–Клапейрона:

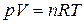, (1)

где – число моль идеального газа;

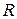– универсальная газовая постоянная (8,314 ).

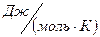Процессом называют любое изменение в системе, приводящее к изменению, по крайней мере, одного из параметров состояния.

Если в результате протекания процесса система возвращается в исходное состояние, то процесс называют круговымили циклическим. Циклические процессы очень часто совершаются в природе и технике, например, двигатель внутреннего сгорания.

Равновесным называют процесс, который протекает медленно, через непрерывный ряд состояний, бесконечно близких к равновесным состояниям. Равновесное состояние – это состояние, которое не изменяется со временем, оно всегда динамическое, но при этом в системе отсутствуют односторонние потоки вещества и энергии, а внутренние параметры (концентрации) имеют одно и то же значение во всей системе. Состояние термодинамического равновесия обусловлено постоянством внешних параметров. В действительности равновесных процессов не бывает.

Обратимый процесс – это процесс, при осуществлении которого в обратном направлении повторяются все промежуточные стадии, а в окружающей среде не происходит никаких изменений.

Необратимый процесс – это процесс, при протекании которого в обратном направлении не повторяется, по крайней мере, одна из промежуточных стадий.

Самопроизвольный процесс – это процесс для протекания которого не требуется затрат энергии извне. Например, переход теплоты от более нагретого тела к телу с более низкой температурой, смешение двух газов и т.п.

Несамопроизвольный процесс требует для своего протекания затрат энергии. Например, при процессе разделения воздуха на кислород и азот обязательно требуется затратить энергию.

Все реальные самопроизвольно протекающие процессы относятся к числу необратимых и неравновесных. Однако чем медленнее они протекают, тем ближе они к обратимым или равновесным процессам.

Состояние системы в термодинамике характеризуют как параметрами, так и функциями состояния. К функциям состояния относят ряд величин, зависящих от параметров состояния системы. Процессы, протекающие в термодинамических системах, характеризуют изменением функций состояния.

Функции состояния системы имеют ряд важных свойств:

1) свойство аддитивности: величина термодинамической функции для всей системы складывается из величин этой функции для определенных ее частей;

2) изменение любой функции состояния определяется только исходным и конечным состоянием системы и не зависит от пути перехода этой системы из исходного в конечное состояние, т.е. определяется разностью значений функции в этих состояниях (т.е. бесконечно малое изменение функции состояния системы является полным дифференциалом);

3) в круговом процессе конечное состояние совпадает с начальным, поэтому любая функция состояния принимает первоначальное значение, а ее изменение в круговом процессе будет равно нулю: .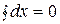

В химической термодинамике важное значение имеет понятие внутренней энергии.

Внутренняя энергия системы – это совокупность всех видов энергии, присущих системе. Внутренняя энергия равна сумме кинетической и потенциальной энергии всех частиц, составляющих данную систему (за вычетом кинетической и потенциальной энергии всей системы в целом):

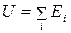, (2)

где 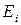– энергия 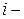го вида движения (поступательного, вращательного, колебательного, электронных переходов и т.д.)

Обмен энергией между системами или между системой и окружающей средой может происходить в виде двух форм: теплоты и работы.

Теплота – форма передачи энергии, связанная с беспорядочным движением частиц. Мера энергии, переданной от одной системы к другой в результате беспорядочного движения частиц – количество теплоты.

В термодинамике принято считать положительной теплоту, полученную системой от окружающей среды, а отрицательной – теплоту, отданную системой.

Если энергия передается путем упорядоченного движения частиц, то совершается работа. Таким образом, величина работы – есть мера энергии, переданной от одной системы к другой при упорядоченном движении частиц системы.

Например, при расширении газа в цилиндре с поршнем молекулы будут иметь составляющую перемещения в направлении движения поршня под действием давления в системе. Или электрическая работа – упорядоченное движения электронов вдоль металлического провода.

Работу, совершенную системой против сил внешнего давления, принято считать положительной, а совершенной над системой – отрицательной.

1.2. Первое начало термодинамики

1.2.1 формулировка и математическая запись I закона термодинамики.

Внутренняя энергия как функция состояния системы

I Закон термодинамики возник в эпоху создания тепловых двигателей. С появлением тепловых машин перед человечеством встала естественная задача создания экономически выгодных машин, в идеале – производящих работу без затрат энергии. Такая машина получила название вечного двигателя I рода. Вечный двигатель I рода – это двигатель, который производит работу без затрат энергии.

Существует несколько формулировок I закона термодинамики:

1) в любой изолированной системе запас внутренней энергии остается постоянным;

2) разные формы энергии переходят друг в друга в строго эквивалентных количествах (закон об эквивалентности различных форм энергии следует из первой формулировки);

3) невозможно получить работу без затрат энергии (другими словами невозможно создание вечного двигателя I рода).

I закон термодинамики следует из более общего закона – закона сохранения энергии: энергия не исчезает и не возникает вновь из ничего при протекании процесса, она лишь может переходить из одной формы в другую в строго эквивалентных соотношениях.

Математическое выражение I закона термодинамики в дифференциальной форме:

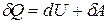
и в интегральном виде: 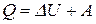(3)

Отсюда следует более конкретная формулировка I закона термодинамики:

Теплота, сообщенная системе расходуется на приращение внутренней энергии и совершение работы.

Использование значков бесконечно малых изменений теплоты и работы подчеркивает, что работа и теплота являются функциями (характеристиками) процесса и существуют, когда есть передача энергии. Перед внутренней энергией стоит знак полного дифференциала, так как 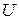является функцией состояния системы, т.к. является величиной аддитивной (см. ур-е (2)) и обладает свойствами полного дифференциала.

Совершаемая в процессе работа часто разделяется на две части:

,

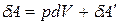где 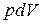– работа расширения или сжатия;

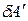– полезная работа (другие виды работы: электрическая, магнитная и пр.).

Уравнение I закона термодинамики с учетом выражения для работы

.

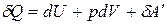Очень часто при протекании термодинамических процессов единственной работой является работа против сил внешнего давления, т.е. работа расширения или сжатия. Тогда уравнение I закона термодинамики принимает вид:

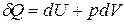(4)

и в интегральном виде: .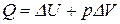

1.2.2. Применение I закона термодинамики к различным процессам

Уравнения I закона термодинамики с калорическими коэффициентами

Из уравнения I закона термодинамики (4) предполагая, что внутренняя энергия системы зависит от ее объема и температуры 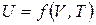, для 1 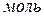идеального газа, получим:

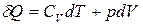. (5)

Из уравнения (4) предполагая, что внутренняя энергия зависит от общего давления и температуры 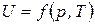, для 1 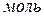идеального газа, получим:

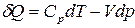. (6)

где 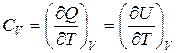– изохорная теплоемкость, показывает, какое количество теплоты необходимо сообщить системе при постоянном объеме, чтобы повысить ее температуру на 1 градус.

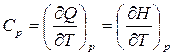– изобарная теплоемкость, показывает, какое количество теплоты необходимо сообщить системе при постоянном давлении, чтобы повысить ее температуру на 1 градус;

Из совместного решения последних уравнений с учетом того, что энтальпия идеального газа, как и его внутренняя энергия, зависит только температуры:

,

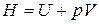а в соответствии с уравнением Менделеева–Клапейрона 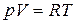, тогда

,

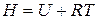получим уравнение взаимосвязи между 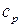и 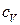для идеального газа.

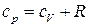. (7)

Рассмотрим систему, в которой протекает какой-либо процесс, единственной работой которого является работа расширения.

1. Изохорный процесс ( 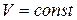). Из уравнения (4), т.к. 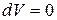, получим

.

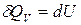После интегрирования получаем:

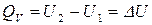. (8)

Из полученного уравнения можно сделать следующие выводы:

а) при протекании изохорного процесса вся теплота, подведенная к системе, расходуется на увеличение ее внутренней энергии;

б) тепловой эффект изохорного процесса обладает свойствами функции состояния: не зависит от пути протекания процесса, а определяется только исходным и конечным состоянием системы.

Работа расширения изохорного процесса равна нулю:

.

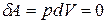2. Изобарный процесс ( 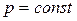). Из уравнения 4, получим:

.

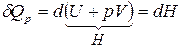В интегральном виде:

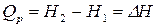. (9)

Из полученного уравнения следуют три важных вывода:

а) существует функция состояния, которую называют энтальпия Н;

б) изменение энтальпии процесса численно равно тепловому эффекту изобарного процесса. Когда теплота передается системе при постоянном давлении, то она расходуется не только на увеличение внутренней энергии системы, но и на совершение работы против сил внешнего давления;

в) тепловой эффект изобарного процесса обладает свойствами функции состояния, т.е. не зависит от пути протекания, а определяется только исходным и конечным состоянием системы.

Работу расширения при изобарном процессе можно рассчитать:

.

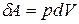Интегрируем в интервале от 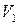до :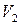

.

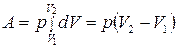Для изобарного процесса, совершающегося в идеальном газе, в соответствии с уравнением Менделеева–Клапейрона (1) для начального и конечного состояния:

,

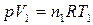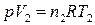
работа расширения равна

.

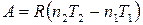Если протекает изобарно-изотермический процесс ( 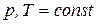), последнее уравнение принимает вид:

.

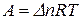3. Изотермический процесс ( 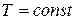), протекающий в идеальном газе. Так как внутренняя энергия идеального газа зависит только от температуры, то при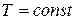 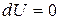, следовательно,

.

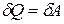или в интегральном виде

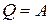. (10)

Таким образом, вся подводимая теплота расходуется на совершение работы или вся работа переходит в теплоту.

Для работы расширения идеального газа, применяя уравнение Менделеева–Клапейрона, получим

.

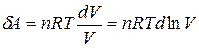После интегрирования и учитывая, что согласно уравнению Менделеева–Клапейрона (1) при 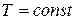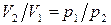, получаем

.

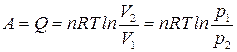4. Рассмотрим процесс, протекающий в изолированной системе или адиабатический процесс ( ).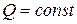

Так как процесс протекает без теплообмена с окружающей средой, то 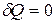. В соответствии с I законом термодинамики для такого процесса получаем:

.

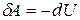и в интегральном виде:

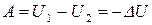. (11)

Из полученного уравнения следует вывод, что в изолированной системе работа может совершаться только за счет убыли ее внутренней энергии.

На основе I закона термодинамики можно получить уравнения состояния идеального газа (уравнения адиабаты):

,

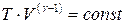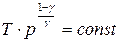, (12)

,

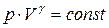где .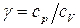

1.3. термохимия

1.3.1. закон гесса

Раздел химической термодинамики, посвященный исследованиям тепловых эффектов различных процессов, называют термохимией.

Теплоту, выделенную или поглощенную системой в ходе какой-либо реакции при отсутствии полезной работы и одинаковой температуре исходных и конечных веществ, называют тепловым эффектом реакции.

Если при протекании реакции отсутствуют любые другие виды работы, кроме работы расширения, то тепловой эффект реакции при 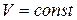равен изменению внутренней энергии (см. ур-е (8)), а при 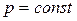– изменению энтальпии (см. ур-е (9)). Так как внутренняя энергия и энтальпия являются функциями состояния системы, то можно сделать следующий вывод:

Тепловой эффект процесса не зависит от пути его протекания, а определяется только исходным и конечным состоянием системы при соблюдении условий:

1) процесс протекает пр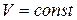и или ;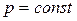

2) в процессе не совершается никаких видов работы, кроме работы расширения или сжатия;

3) температура исходных веществ и продуктов реакции одинакова (в то время как в ходе процесса температура может изменяться).

Это положение было сформулировано на основе проведенных экспериментальных исследований Гессом и называется законом Гесса. Закон Гесса представляет собой прямое следствие из первого закона термодинамики.

Тепловой эффект одного ряда последовательно протекающих реакций равен тепловому эффекту другого ряда последовательно протекающих реакций, если начальные конечные вещества этих двух рядов одинаковы, а процессы протекают при Р,Т = const или при V,T= const.

Из закона Гесса вытекают следствия:

1. В термохимии при написании уравнений принято включать в них тепловые эффекты реакций. Такие уравнения называют термохимическими. Тепловые эффекты реакций определяются не только природой реагирующих веществ, но и их агрегатным состоянием, в связи с чем, в термохимических уравнениях через символы ( 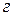), ( ), ( 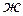) 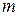обозначаются соответственно газообразное, жидкое и твердое состояния. Например,

.

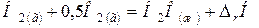Термохимические уравнения обладают всеми свойствами алгебраических уравнений: их можно почленно складывать, вычитать и т.д.

Закон Гесса позволяет вычислить тепловые эффекты тех реакций, для которых непосредственное определение 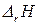связано с большими экспериментальными затруднениями.

Для определения тепловых эффектов реакций с использованием термохимических уравнений составляют термохимические циклы и рассчитывают .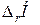

2. Тепловой эффект химической реакции равен сумме теплот образования продуктов реакции за вычетом суммы теплот образования исходных веществ с учетом стехиометрических коэффициентов.

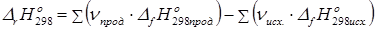(13)

Теплотой образования вещества называют тепловой эффект реакции синтеза
1 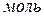сложного соединения из простых веществ. Теплоты образования простых веществ ( 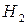, 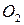и др.) принимают равными нулю. Стандартная теплота образования обозначается: 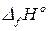. Буква 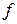от английского слова 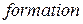– образование.

3. Тепловой эффект химической реакции равен сумме теплот сгорания исходных веществ за вычетом суммы теплот сгорания продуктов реакции с учетом стехиометрических коэффициентов.

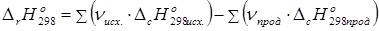. (14)

Теплотой сгорания вещества называют тепловой эффект химической реакции полного сгорания 1 моль данного вещества молекулярным кислородом. Теплоты сгорания углекислого газа и воды принимают равными нулю. Стандартная теплота сгорания обозначается: 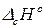. Буква 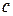от английского слова 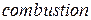– сгорание.

В справочной литературе приведены величины теплот образования и теплот сгорания важнейших химических веществ в стандартных условиях. За стандартные условия принято давление, равное 1 атм. и температура 298 .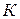

1.3.2. влияние температуры на тепловые эффекты химических