В изолированной системе

Рассмотрим какую-либо изолированную систему. Для изолированной системы 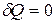. С учетом этого уравнение II закона термодинамики имеет вид:

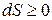. (21)

Из выражения (21) следует, что при протекании обратимого равновесного процесса энтропия остается постоянной. Условием самопроизвольного протекания процесса в изолированной системе является неравенство 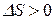, т.е. возрастание энтропии. Процессы, сопровождающиеся уменьшением энтропии ( 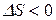) в изолированной системе неосуществимы. Если же протекание процесса возможно как в прямом, так и в обратном направлении, в изолированной системе процесс будет протекать в том направлении, которое сопровождается увеличением энтропии.

При протекании самопроизвольных процессов в изолированной системе одновременно с увеличением энтропии система приближается к состоянию равновесия. Когда система достигнет состояния равновесия, все процессы прекращаются и энтропия становится максимальной. Условие равновесия в изолированной системе можно записать математически:

.

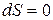
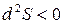Если система сложная, то в отдельных ее частях энтропия может уменьшаться, а в других увеличиваться, однако общая энтропия системы при этом должна увеличиваться.

1.4.3. расчет изменения энтропии при протекании различных