Логистические модели цивилизационной динамики

Результаты многочисленных и разноплановых исследований свидетельствуют, что конкурирующие за общие ресурсы системы (цивилизации, этносы, экономические формации, промышленные компании и т.п.) подобно живым организмам проходят в своем развитии четыре основные стадии (фазы): зарождения, молодости, зрелости и старости. Продолжительность активной жизни реальных систем зависит от множества разнообразных внешних и внутренних факторов. Большую роль при этом играют процессы конкурентных взаимодействий. Указанные взаимодействия могут носить опосредованный (через общий ресурс) и потому достаточно мирный характер, но могут быть и антагонистичными, сопровождающимися взаимоуничтожением. И если в первом случае наибольшие шансы на выживание имеет наиболее эффективная (в смысле целесообразности использования запасов ресурсов) система, то во втором случае многое зависит от интенсивности подавления одной конкурирующей системы другой.

В настоящем параграфе мы рассмотрим лишь некоторые из возможных и, может быть, наиболее простые формальные модели динамики такого рода взаимодействий, основывающиеся на логистических уравнениях.

Пусть изменение переменной состояния некоторой системы (например, цивилизации) с течением времени описывается уравнением вида

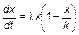, (3.3.21)

где x – переменная состояния (например, валовой продукт, производимый системой в единицу времени); k – общий объем запасов ресурса, который может быть израсходован в обеспечение производства продукта, другими словами, k – это предельная по x емкость среды существования цивилизации (этноса, формации и т.п.), lλ_i – параметр, определяющий интенсивность производства валового продукта (воспроизводства) системы i.

Решение этого уравнения при λl = const, k = const имеет вид

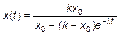. (3.3.22)

Это решение описывает так называемую логистическую кривую (рис. 3.3.3).

Рис. 3.3.3. Логистическая кривая

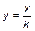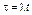Заметим, что путем замены и уравнение может быть представлено в безразмерной форме

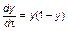. (3.3.23)

Уравнение (3.3.23) имеет две точки равновесия: y₁ = 0 и y₂ = 1. Точка y₁ = 0 является точкой неустойчивого равновесия, а точка y₂ = 1 – устойчивого.

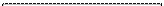Учитывая конечную длительность проявления системы как единой целостной реальности, уравнение (3.3.21) мы в принципе должны записывать в виде

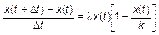. (3.3.24)

Преобразуя (3.3.24), получаем

.

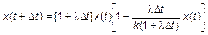Обозначив

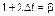β, (3.3.25)

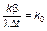. (3.3.26)

Находим

.

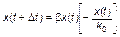Принимая в качестве единицы измерения времени величину DΔt (т.е. вводя дискретное время) и обозначая

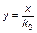, (3.3.27)

получаем логистическое уравнение в дискретной форме

y_n+1 = bβy_n(1 – y_n). (3.3.28)

Уравнение (3.3.28) при bβ > 1 имеет две точки равновесия: y₁ = 0 и 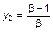. Для определения устойчивости отображения y_n+1 = ƒf (y_n) необходимо определить величину 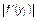в точке равновесия. Если окажется, что 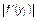· 1 > 1, то точка равновесия 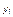будет неустойчива (последовательность …... 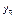, , 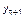...… будет расходиться). Очевидно, при 1 < bβ < 3 точка равновесия 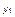является неустойчивой, а точка равновесия 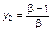– устойчива. При bβ > 3 вторая точка равновесия также становится неустойчивой. При 3 > b > 4 уравнение (3.3.28) описывает множество многопериодических и хаотических движений. При b = 3 величина y_n повторяется через каждую итерацию, т.е. устойчивым является движение с удвоенным периодом. При дальнейшем увеличении bβ двупериодическое движение становится неустойчивым, но устойчивым становится движение с периодом 4, которое далее замещается устойчивым циклом с периодом 8 при больших значениях bβ и т.д. Процесс удвоения периода повторяемости продолжается до тех пор, пока bβ не достигнет предельного значения β_∞b_¥ = 3,56994... . При b > b_¥β_∞ могут возникать хаотические движения. Вблизи βb_¥∞ значения параметра bβ, при которых происходит удвоение периода, подчиняются универсальному закону Фейгенбаума (справедливому, кстати, и для других более сложных отображений ).

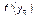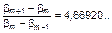(3.3.29)

В области b_¥ < bβ < 4 существуют также достаточно узкие полоскиΔβ, которым отвечают периодические движения.

Предположим, что область возможных ресурсов для системы 2 включает в себя область возможных ресурсов системы 1 (рис. 3.3.4)

Рис. 3.3.4. Области ресурсов систем 1 и 2 (K₂ É K₁)

Согласно схеме рис. 3.3.4 в пределах области K₁ рассматриваемые системы являются конкурирующими. Такого рода ситуация может, например, возникнуть тогда, когда система 2 окажется более эффективной (более разнообразной) в смысле используемых ею ресурсов. Поскольку K₂ É K₁, то в области K₁ системы 1 и 2 являются конкурирующими. Данное обстоятельство можно учесть, в частности, следующим образом:

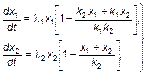(3.3.30)

где k₁ и k₂ – соответственно ресурсные емкости областей K₁ и K₂.

Заметим, что в описываемой здесь модели также предполагается, что производительность lλ₂ не зависит от области используемого ресурса (K₁ или K₂).

Обозначая

, ,

, _,

,

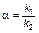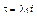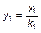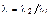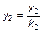переходим к системе безразмерных уравнений:

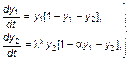(3.3.31)

где, очевидно, αa < 1.

Решение системы уравнений (3.3.31) выглядит следующим образом (рис. 3.3.5).

Время вытеснения одной цивилизации другой зависит от параметров lλ₁ и αa.

Фазовый портрет системы (3.3.31) при 0 < aα < 1 содержит три типа точек равновесия: устойчивый (y₁ = 0, y₂ = 1) и неустойчивый (y₁ = y₂ = 0) узел и седло (y₁ = 1, y₂ = 0) (рис. 3.3.6, а).

По мере приближения параметра aα к 1 область сгущения траекторий, притягивающихся к точке (0, 1), все более и более сжимается и при aα = 1 превращается в прямую линию. При этом происходит бифуркация, в результате которой линия, соединяющая точки (0, 1) и (1, 0), превращается в континуум пар «устойчивый узел – седло» (рис. 3.3.6, б). Все траектории, приходящие из бесконечности и из неустойчивого узла (0, 0), замыкаются теперь на этой прямой.

Рис. 3.3.5 Зависимость объема производства валового продукта
двух конкурирующих систем от времени:
а – безразмерные переменные; б – размерные переменные;
x = x₁ + x₂ – суммарный объем производства валового продукта

а б

Рис. 3.3.6. Фазовые портреты системы двух опосредованно
конкурирующих систем: а – 0 < a < 1; б – a = 1; о – точки равновесия

Траектории, пересекающие линию, соединяющую точки (0, 1) и 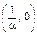на рис. 3.3.6, а, имеют касательные в точке пересечения 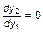, а траектории, пересекающие линию y₂ = y₁, – соответствующие касательные .

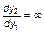Траектории, пересекающие линию y₂ = y₁ на рис. 3.3.6, б, имеют касательные в точке пересечения .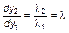

Увеличение aα в сторону значений, больших 1, с содержательной точки зрения означает переход к системе уравнений

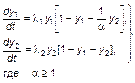(3.3.32)

Указанный переход обусловлен тем, что при aα > 1 ресурсная область K₂ оказывается включенной в область K₁. При этом в фазовом пространстве точка (0, 1) становится седлом, а точка (1, 0) превращается в устойчивый узел.

Если моделируется процесс вытеснения одной системы другой в рамках единой метасистемы (например, в рамках одной экономики), то весьма важным показателем становится суммарный объем производства продукта x = x₁ + x₂ (рис. 3.3.5, б), производимый обеими системами вместе. Приведенная нами модель взаимодействий сравнительно просто распространяется на большее количество конкурирующих систем (цивилизаций, формаций, экономических систем, популяций биологических организмов, социальных групп языков и т.д.).

Следует также заметить, что максимальное по времени значение x₁(t) зависит не столько от сочетания параметров λl₁, λl₂ и aα, сколько от соотношения начальных значений x₁₀ и x₂₀.

При рассмотрении эволюции опосредованно конкурирующих систем обычно учитывается тот опытный факт, что наиболее эффективные, наиболее разнообразные в своих ресурсных источниках системы зарождаются существенно позднее менее эффективных, менее разнообразных. Это позволяет упорядочить начальные значения соответствующих переменных следующим образом:

x_-01 >> x_-02 >> x_-03 >> ... >> x_-0n, (3.3.33)

где из двух конкурирующих систем i и j более сильной является система с большим номером, т.е. из условия

(K_i > K_j) ® (i > j). (3.3.34)

Указанная закономерность зарождения более сильных систем объясняется тем, что проблема повышения эффективности производства обобщенного продукта x возникает тогда, когда возможности его роста в старой системе оказываются исчерпанными, т.е. старая система в своей эволюции выходит на логистическое плато.

Дискретный (по времени) аналог описанной выше модели выглядит следующим образом:

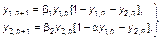(3.3.35)

Вполне очевидно, что в этом случае в системе взаимодействующих систем становятся возможными и более сложные виды движений: периодические и хаотические.

Определим возможные точки равновесия системы (3.3.35), для чего положим

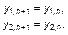
С учетом (3.3.35) получаем

y_1,n = bβ₁y_1,n [1– y_1,n– y_2,n],

y_2,n = βb₂y_2,n [1– αay_1,n– y_2,n].

Первая точка равновесия, очевидно, как и ранее, – начало координат, y_1,n = y_2,n = 0. Вторая – y_1,n = 0, y_2,n = (b₂ – 1) / b₂. Третья – y_1,n = (b₁ – 1) / b₁, y₂ = 0. Четвертая точка равновесия находится из условия y_1,n ¹ 0 и y_2,n ¹ 0. Ее координаты оказываются равными

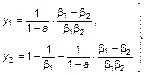(3.3.36)

В силу того, что величина b₁ обычно меньше величины b₂, то четвертая точка равновесия, как правило, содержательного интереса не представляет.

Для определения характера состояния равновесия в оставшихся трех точках необходимо вычислить производные трех правых частей отображений:

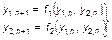
в соответствующих точках. В результате получим:

точка (0,0)	, , , ;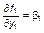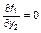
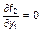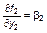точка (1,0)	, , , ;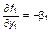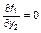
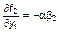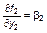точка (0,1)	, , , .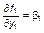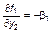

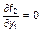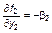Точка равновесия будет неустойчивой, если хотя бы одна из соответствующих ей частных производных удовлетворяет условию

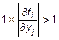. (3.3.37)

При выполнении (3.2.37), как уже отмечалось ранее, в силу дискретности шага по времени последовательность соответствующих переменных начнет расходиться (а возможно, и будет совершать некоторые периодические движения). Согласно представленным выше расчетам условия появления периодических движений, удвоения периодичности, появления хаоса опять связаны с параметрами b_i. Если b_i < 1, то точка равновесия устойчива, если хотя бы одно из b_i > 1, то точка равновесия неустойчива.

Дополним систему уравнений (3.3.30) членами, описывающими взаимоподавление систем. В результате получим

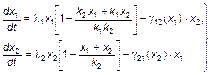(3.3.38)

Пусть, например, обменные члены в (3.3.38) имеют вид

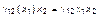, (3.3.39)

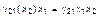. (3.3.40)

Тогда систему (3.3.38) можно преобразовать к виду

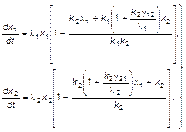
Или, обозначая

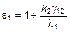, (3.3.41)

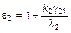, (3.3.42)

получаем

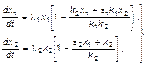(3.3.43)

где eε₁ и eε₂ – параметры, характеризующие интенсивность антагонистических, взаимоуничтожающих взаимодействий.

Или, переходя к безразмерной форме, получаем следующую более простую систему уравнений:

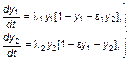(3.3.44)

где 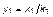, , 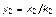, 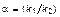eε = eε₂αa.

Очевидно, εe₁ ³ 1, εe₂ ³ 1, 0 £ εe.

Количество независимых параметров в системе (3.3.44) можно еще сократить, введя новую переменную времени

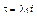(3.3.45)

и обозначив

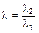. (3.3.46)

Тогда вместо (3.3.44) будем иметь

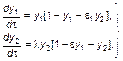(3.3.47)

Точками равновесия системы (3.3.47) будут следующие: (0, 0); (0, 1); (1, 0) и 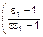, 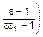. Последняя точка существует в области неотрицательных значений y₁ и y₂ только в случае εe > 1. Как и ранее, первая точка (0, 0) является неустойчивым узлом, точка (0, 1) – устойчивым. Но в отличие от предыдущего точка (1, 0) является не седлом, а тоже устойчивым узлом. Новая же четвертая точка 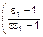, 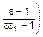есть седло. При стремлении eε₂ к 1 (εe ® 1/aα) четвертая точка сливается с точкой (1, 0), превращая ее в седловую (происходит бифуркация). Аналогично при стремлении e₁ ® 1 и εe > 1 такое слияние происходит с точкой (0, 1). Фазовый портрет рассматриваемой системы представлен на рис. 3.3.7.

Рис. 3.3.7. Фазовый портрет системы
двух взаимоуничтожающих цивилизаций при εe > 1: о – точки равновесия

Возможность превращения (за счет слияния) устойчивого узла (0, 1) в седло свидетельствует о том, что в случае отсутствия противодействия со стороны потенциально более сильной системы (например, более сильного этноса) последняя может быть полностью уничтожена. В промежуточном случае eε₁ > 1 и eε > 1, в зависимости от начальных условий возможны победы как более сильной системы, так и более слабой. Компромиссное состояние равновесия является неустойчивым. Борьба систем идет до полного подавления одной из них. Исторических примеров, описывающих подобные ситуации, можно привести великое множество.

В качестве дискретного аналога модели (3.3.47) можно рассматривать систему логистических уравнений вида

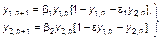(3.3.48)

или

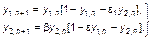(3.3.49)

Очевидно, что данная система уравнений в зависимости от сочетания параметров eε₁, eε и βb, а также в зависимости от начальных условий y₁₀ и y₂₀ может порождать не только представленные выше эволюционные процессы, но и процессы периодические и хаотические. Последнее во многих случаях делает результат антагонистических взаимодействий двух систем непредсказуемым.

С системно-физической точки зрения хаос возникает в случае, когда перед системой, поведение которой подчиняется некоторому экстремизационному принципу (закону), возникает ситуация многозначного выбора, удовлетворяющего этому принципу (закону). Другими словами, экстремизационный характер ценностного принципа не всегда однозначно определяет выбор конкретной реакции системы.

Хаос есть проявление «замешательства» системы, обусловленного неоднозначностью выбора. И когда такой выбор становится многозначным, возникает хаотическое движение, которое можно рассматривать как периодическое с бесконечным большим периодом повторяемости.

В процессах конкурентных взаимодействий логистических систем (т.е. систем, имеющих предельный уровень развития) хаос возникает, как правило, при выходе одной их них на эволюционное плато (рис. 3.3.8).

Рис. 3.3.8. Зависимость валового продукта
трех взаимодействующих цивилизаций:
ЭП – эволюционное плато, t₁, t₂, t₃ – моменты времени
«реального» проявления соответствующих структур

В заключение данного параграфа приведем еще одну из цивилизационных моделей – модель гонки вооружений Ричардсона. Система уравнений модели в простейшем случае (две конкурирующие страны или группы стран) выглядит следующим образом:

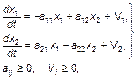(3.3.50)

где x_i – объем вооружений (точнее, боевая мощь вооружений) i-й оперирующей стороны; V_i – некоторый постоянный стимул роста вооружений, независящий от уровня вооружений противоборствующей стороны. Отрицательные слагаемые в (3.3.50) описывают моральное и физическое старение вооружений.

Вводя обозначения

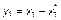, (3.3.51)

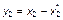, (3.3.52)

где 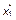и 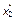удовлетворяют условиям

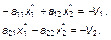
система (3.3.52) легко преобразуется к виду

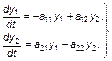(3.3.53)

Характеристическое уравнение этой системы имеет два вещественных корня

.

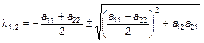Причем если

a₁₂a₂₁ > a₁₁a_22, (3.3.54)

то один из корней будет положительным. Таким образом, если взаимовлияние (включая подозрительность) двух стран будет достаточно велико (a₁₂ и a₂₁ относительно большие числа), то в системе двух стран (или двух коалиций стран) будет наблюдаться экспоненциальный рост вооружений. Если же указанное влияние не очень значительно (a₁₂a₂₁ < a₁₁a₂₂) (т.е. рассматриваемые страны не видят друг в друге большой опасности), то объемы вооружений этих стран будут экспоненциально приближаться к соответствующим предельным значениям при t ® ¥: 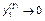, т.е. 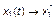, , 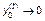т.е. .

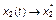С учетом предельных ресурсных возможностей участников гонки вооружений модель (3.3.50) может быть преобразована в связанную систему логистических уравнений

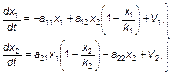(3.3.55)

где k₁ и k₂ – параметры, характеризующие предельные ресурсные возможности соответствующих стран.