Возрастная динамика населения

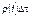Пренебрегая социальной неоднородностью и половыми различиями, обозначим через количество индивидов, имеющих в момент времени t возраст в интервале от 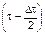до . Тогда приращение величины rρ(t, tτ)DtΔτ за время ΔDt будет равно

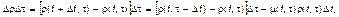(3.3.56)

где μm(t, τt) – средний темп смертности населения в возрасте tτ в момент времени t. Разлагая функцию 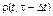в ряд 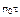и ограничиваясь первыми двумя членами, получим

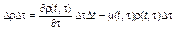. (3.3.57)

Поскольку старение индивида, имеющего в момент времени t возраст τt, за время ΔDt происходит именно на эту величину, то

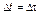Δτ. (3.3.58)

При из (3.3.57) получаем основное уравнение демографической динамики (возрастной динамики населения)

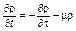. (3.3.59)

Общая численность населения на рассматриваемой территории в момент времени t будет, очевидно, равна

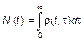. (3.3.60)

Если данная территория открыта с точки зрения миграции населения, то уравнение (3.3.59) необходимо дополнить соответствующим слагаемым. В результате будем иметь

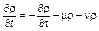, (3.3.61)

где n – средний балансовый удельный темп миграции (при νn > 0 миграционный поток из системы превышает миграционный поток в систему и наоборот).

Пусть внешние и внутренние факторы, влияющие на демографическую ситуацию, давно стабилизировались так, что установилось равновесие

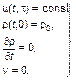(3.3.62)

Тогда из (3.3.59) получаем

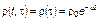. (3.3.63)

Таким образом, в случае, если темп смертности не зависит от возраста и отсутствуют какие бы то ни было возмущения, демографическая кривая является экспоненциальной. Общая численность населения при этом согласно (3.3.60) оказывается равной

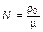. (3.3.64)

Величина N, как и следовало ожидать, в данном случае не зависит от t.

Пусть теперь смертность является возрастающей функцией возраста вида

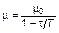, (3.3.65)

где параметры μm₀ и T предполагаются постоянными.

Очевидно, величина T играет роль порога, ограничивающего сверху среднюю продолжительность жизни.

Подставляя (3.3.65) в (3.3.59), находим

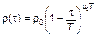. (3.3.66)

В этом случае отношение ρr(tτ)/rρ₀ стремится к нулю по мере приближения возраста tτ к его критическому значению T. Такое поведение распределения rρ(t, tτ) (демографической кривой) объясняется катастрофическим ростом смертности (m ® ¥∞) по мере приближения к предельному возрасту T.

Общая численность населения в данном случае равна

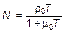. (3.3.67)

При этом, как и раньше, величина N от времени не зависит.

Пусть теперь

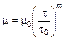. (3.3.68)

При тех же исходных условиях получаем

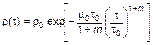. (3.3.69)

В случае положительных (что вполне естественно) значений постоянной m мы имеем более крутое, чем экспоненциальное, падение кривой распределения населения по возрасту. Однако она также имеет затянутый до ¥∞ «хвост».

Рассмотрим теперь случай нестационарного распределения. Возникновение нестационарных режимов может быть вызвано самыми различными причинами. Среди них можно, например, выделить такие, как колебания рождаемости (смертности), людские потери во время войн и вооруженных конфликтов, миграция населения, потери населения на производстве и транспорте, потери от эпидемий, смертельно опасных заболеваний и голода.

Из сказанного вытекает, что уравнения (3.3.59), (3.3.61) не являются замкнутыми. Чтобы их замкнуть, надо к ним добавить уравнение, определяющее величину rρ₀. В простейшем случае однородной в социальном, профессиональном и половом отношении популяции будем иметь

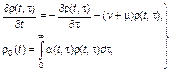(3.3.70)

где aα(t, τt) – удельный темп рождаемости в возрастной группе tτ в момент времени t.

Предположим теперь, что отклонения демографической кривой от ее стационарного положения невелики и носят характер возмущений, которые можно представить в виде

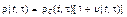, (3.3.71)

где ρr_с(t, τt) = ρr(τt) – стационарное решение уравнения (3.3.59) или (3.3.61); u(t, τt) – относительно небольшое нестационарное возмущение. Подставляя (3.3.71) в первое уравнение системы (3.3.70) при n ν= 0 и учитывая, что 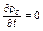, будем иметь

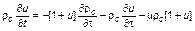. (3.3.72)

Так как

,

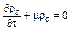то

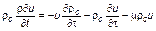
или

.

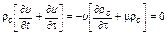Откуда окончательно

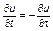. (3.3.73)

Уравнение (3.3.73) является справедливым только в том случае, если возмущение ρr(t, τt) является функцией запаздывающего аргумента (t – tτ), т.е.

u(t, τt) = u(t – tτ). (3.3.74)

Таким образом мы получили весьма интересный и практически широко известный результат, свидетельствующий о возможности возникновения и распространения демографической волны. Согласно (3.3.73) возмущение, возникшее в некоторой возрастной группе с течением времени распространяется, повторяясь, вверх по лестнице возрастов.

Следует, однако, заметить, что при получении решения (3.3.74) мы еще не учли положительной обратной связи рождаемости, которая задается вторым уравнением системы (3.3.70) и которая обеспечивает появление вторичных, третичных и т.д. демографических волн. Для упрощения анализа предположим, что воспроизводящими являются только индивиды, имеющие возраст τt₀, т.е.

aα(t, τt) = αa₀δd(τt – τt₀), (3.3.75)

где δd(t – τt₀) – δd-функция (dδ(x ¹≠ 0) = 0, δd(x = 0) = ∞¥); αa₀ – const. С учетом этого предположения второе уравнение системы (3.3.70) будет выглядеть так:

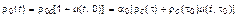. (3.3.76)

Отбрасывая стационарную составляющую, получаем

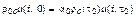. (3.3.77)

Поскольку

u(t, tτ₀) = u(t – τt₀),

то возмущение начальных условий будет происходить периодически в момент прохождения демографической волны через активную в смысле воспроизводства группу населения. Таким образом, в рамках данного приближения демографическая волна будет периодически (с периодом tτ₀) повторяться. В реальной жизни в силу того, что воспроизводящей группой населения является не одна возрастная группа, а целое множество возрастных групп, демографическая волна, получающаяся в последующем как результат сложения многих волн с разными периодами τt₀ и разными амплитудами, начинает постепенно размываться. В этом смысле «раны», нанесенные возрастной стратификации населения войной или какими-либо другими бедствиями, постепенно затягиваются. При отсутствии значительных возмущений распределения rρ(t, τt) опять начинает приближаться к равновесному (стационарному) rρ_с(τt).

Знание средних периодов прохождения, глубины (амплитуды) и длительности демографических волн является чрезвычайно важным с точки зрения решения социальных, экономических и технологических проблем как в масштабах отдельно взятого региона, так и всей страны в целом. Каковы тенденции изменения доли трудоспособного населения, каковы тенденции изменения численности подрастающего поколения и численности пенсионеров – все это весьма существенные вопросы управления обществом. На рис. 3.3.9 в качестве примера приведены эмпирические данные (кривые 1 и 2) о распределении населения США по возрастам в 1870 г. и 1984 г.

На представленных графиках хорошо заметны повторяющиеся демографические волны (в частности, «беби-бум» 1950–1965 гг., что соответствует t ~ 20–35 лет на кривой 1984 г.). Сравнение данных за 1870 г. и 1984 г. указывает на значительное вмешательство общества в развитие демографической ситуации (приближение эмпирического распределения в среднем к почти линейному закону обусловлено, в первую очередь, ростом материального благополучия граждан и успехами медицины).

Рис. 3.3.9. Распределение населения США по возрастам в 1870 г. и в 1984 г.:
1 – распределение для 1984 г., 2 – для 1870 г.;
3 – теоретическое распределение 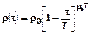при T ≈» 100, μm₀ ≈» 0,01;
4 – теоретическое распределение 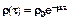при μm » 0,03

В общем случае, с учетом неоднородности возрастных групп по различным конфессиональным, социальным, экономическим, профессиональным, национальным, физико-геогра­фическим (территориальным и т.д.) признакам, модель демографической динамики становится существенно более сложной:

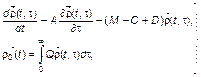(3.3.78)

где А – матрица переходов из одних социальных групп в другие в связи с изменением возраста; М – матрица (диагональная) удельных темпов смертности; С – матрица интенсивностей переходов из одних социальных групп в другие внутри одной возрастной категории; D – матрица интенсивностей (темпов) миграции; Q – матрица удельных темпов рождаемости; 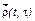– вектор распределения населения по возрастным половым, национальным, профессиональным и иным группам.

Зная матрицы A, M, C, D и Q, их зависимость от времени, с помощью (3.3.78) можно осуществлять моделирование структурной динамики народонаселения. Знание социально-возрастной стратификации позволяет, в частности, решать задачи анализа тенденций изменения качества населения. С помощью такого типа моделей возникает возможность прогнозирования таких социально опасных явлений, как наркомания, алкоголизм, дебилизация и т.п.

Рождаемость и смертность зависят от целого ряда факторов, в том числе и от возраста t (рис. 3.3.10–3.3.11).

Рис. 3.3.10. Зависимость темпов смертности от возраста (США, 1957г., [8])

Рис. 3.3.11. Зависимость среднего темпа рождаемости
от валового национального продукта в расчете на душу населения
(~ 1970-е гг.)

Как свидетельствуют многочисленные эмпирические исследования, средняя ожидаемая продолжительность жизни в значительной степени определяется уровнем питания населения (рис. 3.3.12).

Рис. 3.3.12. Зависимость средней ожидаемой продолжительности жизни
от уровня питания

Как видно из предыдущего рассмотрения, средняя ожидаемая продолжительность жизни определяется не только существующими в данный момент темпами рождаемости и смертности, но и видом демографической кривой, сложившейся к этому моменту времени. Темпы же рождаемости и смертности, помимо отмеченных ранее, зависят и от множества других существенных факторов. Среди них, прежде всего, следует отметить экологические, психологические, технологические (например, наличие существенной разницы в темпах рождаемости и смертности в промышленных и сельскохозяйственных районах), социальные и другие факторы. Значительное влияние на демографическую ситуацию оказывают такие явления, как наркомания, алкоголизм, СПИД и т.п.