ЛЕКЦИЯ 24. Синтез оптимальных систем.

В случае, когда не только помеха, но и задающее воздействие являются случайными функциями времени возникает общая задача оптимального синтеза. Это задача оптимизации структуры и параметров системы. На вход проектируемой системы действуют стационарные сигнал и помеха, автокорреляционные функции которых известны. Математические ожидания сигнала и помехи равны нулю. Желаемый выходной сигнал синтезируемой системы определяется заданной частотной характеристикой. Необходимо найти передаточную функцию системы, при которой суммарная средняя квадратическая ошибка системы минимальна :

^_e = e ² ( t ) = min

где : e ( t ) = yж ( t ) - y ( t ) - ошибка системы ;

yж ( t ) - желаемый выходной сигнал системы ;

y ( t ) - выходной сигнал ( реальный ).

Рассмотрим задачу оптимальной фильтрации. В этом случае :

W_ж (jw) =1, т.е. yж ( t )= x ( t ).

Дисперсия ошибки :

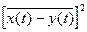^ ^_х + ^_у - ^_ху

где s ²_х - ошибка по сигналу ;

s ²_у - ошибка по помехе ;

s ²_ху - взаимная ошибка сигнала и помехи.

Дисперсию выходного сигнала по помехе найдем так :

s ²_у =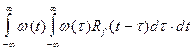

где : w ( t ) - импульсная переходная функция системы

R _f ( t ) - автокорреляционная функция суммарного входного сигнала

f ( t ) = x ( t ) + n ( t ) .

Для взаимной ошибки :

s ²_ху =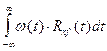

где : R _{x f} ( t ) - взаимная корреляционная функция сигнала с суммарным воздействием.

Синтез оптимальной системы сводится к нахождению импульсной переходной функции w ( t ) .

Решение этой задачи во временной области является сложной задачей. Значительно проще решить ее в частотной области, т.е. найти оптимальную частотную характеристику системы :

W ₀ ( j w ) =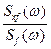

где : S _f (w ) - спектральная плотность спектрального сигнала на входе проектируемой системы ;

S _{x f} (w) - взаимная спектральная плотность сигнала с помехой.

Если сигнал и помеха некоррелированы, то :

S _{x f} (w ) = S _x(w )

S _f (w ) = S _x (w ) + S _n (w ) .

Из выражений следует, что оптимальная частотная характеристика выделяет составляющие сигнала на частотах, на которых его спектральная плотность сравнительно велика, и ослабляет составляющие сигнала на частотах с максимальной спектральной плотностью помехи.

С учетом оптимальной частотной характеристики минимальное значение дисперсии ошибки для некоррелированных сигнала и помехи будет равно :

s² _min =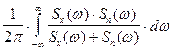

Таким образом, если спектры сигнала и помехи не перекрываются, то средняя квадратическая ошибка может быть равна нулю .

Дисперсия ошибки s² _min определяет потенциальную точность оптимальной системы при заданных спектральных плотностях сигнала и помехи, т.е. теоретическую нижнюю границу дисперсии ошибки, определяемую лишь расчетным путем, но не достижимую ни для какой реальной системы.

При проектировании систем автоматического управления часто возникает ситуация, когда оптимальный синтез проводится при условии, что система должна содержать функциональные элементы с заданными неизменяемыми характеристиками. Например, при проектировании исполнительного устройства выбор двигателя с редуктором определяется требованиями, несвязанными с задачей оптимального синтеза, и характеристики этих устройств на стадии оптимального синтеза системы являются заданными.

Таким образом, возникает задача оптимального синтеза при наличии в составе проектируемой системы заданной неизменяемой части. В этом случае оптимизация структуры системы осуществляется посредством корректирующих цепей.

Рассмотрим использование для оптимизации структуры системы последовательной корректирующей цепи.

Если W_н ( Р ) - передаточная функция неизменяемой части системы, W_к ( Р ) - передаточная функция последовательной корректирующей цепи, то передаточная функция разомкнутого контура этой системы :

W ( Р ) = W_н ( Р ) W_к ( Р ).

Потребуем, чтобы W ( Р ) = W_опт ( Р ).

W_опт ( Р ) - передаточная функция системы, полученная в результате оптимального синтеза.

W_к ( Р ) = W_опт ( Р ) / W_н ( Р ).

Функция W ( Р ) стремящаяся к W_опт ( Р ), реализуется как правило лишь приблизительно, т.к. зачастую W_к ( Р ) приводит к физически нереализуемой динамической системе .

На рисунке изображена экстремальная характеристика объекта управления, на которую действует поисковый сигнал. Если сигналу управления соответствует точка 1 экстремальной характеристики, то на входе объекта управления появляется сигнал, совпадающий по фазе с поисковым сигналом, если мы попадаем в точку 2 , то сигнал на выходе объекта управления имеет противоположную среду. Если попадаем в точку 3 , то на выходе появляется отрицательная составляющая сигнала, достигающая максимума в точке экстремума.

Рассмотрим систему адаптации в виде системы управления виброиспытаниями при полигармоническом возбуждении вибраций :

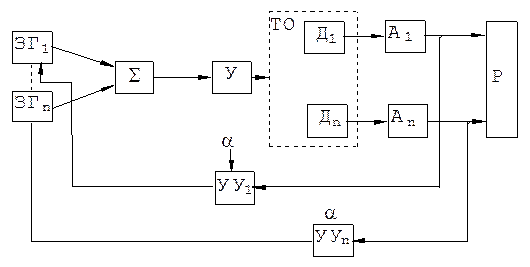
ТО - технологический объект ;

У - усилитель ;

АК - анализаторы качества ;

Д - датчик виброперегрузок ;

УУ - управляющие устройства ;

ЗГ - задающие генераторы ;

a - опорные напряжения ;

Р - блок регистрации.

Управляющее устройство i-го канала сравнивает оценку сигнала анализатора качества с i-ым опорным напряжением, выделяет ошибку, которая преобразуется исполнительным органом и перестраивает амплитуду опорного сигнала i-го задающего генератора до тех пор, пока оценка не сравняется с опорным напряжением a_i .

Это равносильно стабилизации амплитудно-частотной характеристики тракта « задающий генератор - анализатор качества » на всех частотах w_i .