Синтез системы при заданной структурной схеме.

При заданной структурной схеме задача синтеза заключается в том, что при известных характеристиках сигнала и помехи нужно определить оптимальные значения параметров системы, при которых суммарная средняя квадратическая ошибка минимальна. В этом случае она является функцией параметров системы : s²_е = f (b₁, b₂, ... b_n ) ,

где b_i - параметры схемы.

Для расчета оптимальных значений параметров нужно исследовать эту функцию на минимум, т.е. решить следующую систему уравнений :

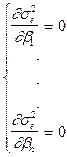
В процессе синтеза системы автоматического управления обычно требуется вычислить оптимальные значения только настраиваемых параметров ( коэффициент усиления, постоянная времени корректирующего устройства ). Число этих параметров невелико, что облегчает задачу оптимизации.

Пример.

Найти оптимальное значение коэффициента усиления системы автоматического управления, передаточная функция которой в разомкнутом состоянии равна :

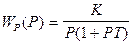
На систему действуют сигнал и помеха со спектральными плотностями :

Суммарная средняя квадратическая ошибка системы равна :

где : 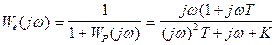- частотная характеристика ошибки системы ;

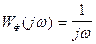- частотная характеристика формирующего фильтра сигнала ;

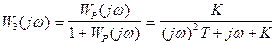- частотная характеристика замкнутой системы.

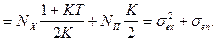
Оптимальное значение коэффициента усиления определяется из условия экстремума :

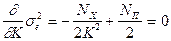
Оптимальный коэффициент усиления :

K_opt =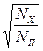

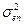- среднеквадратическая ошибка действия помехи.

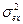- среднеквадратическая ошибка относительного сигнала.

Оптимальная полоса пропускания.

Рассмотрим систему с частотной характеристикой в виде :

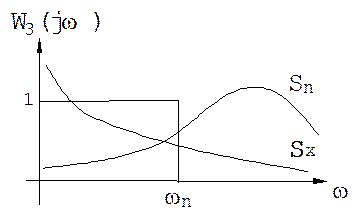
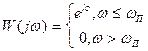
Если сигнал и помеха некоррелированы, то дисперсия ошибки такой системы равна :

.

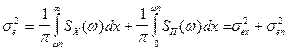где S_x (w ) - спектральная плотность сигнала,

S_n (w )- спектральная плотность помехи.

Полоса пропускания системы автоматического управления, при которой средняя квадратическая ошибка принимает минимальное значение, называют оптимальной.

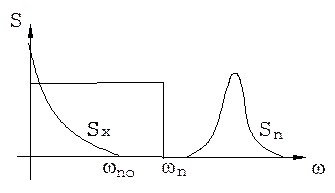
Если графики спектральных плотностей сигнала и помехи не перекрываются, то оптимальная полоса пропускания системы равна граничной частоте спектра сигнала. В этом случае s²_е = 0 , т.к. все составляющие спектра сигнала воспроизводятся системой и ни одна составляющая спектра помехи не проходят на ее выход.

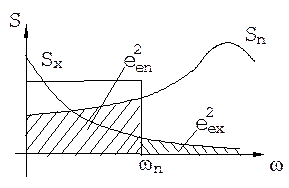
Если графики спектральных плотностей сигнала и помехи перекрещиваются, составляющие s²_ех и s²_еп не равны нулю.

Первая составляющая определяется той частью спектральной плотности сигнала, которая расположена за полосой пропускания системы. С расширением полосы пропускания эта составляющая ошибки уменьшается.

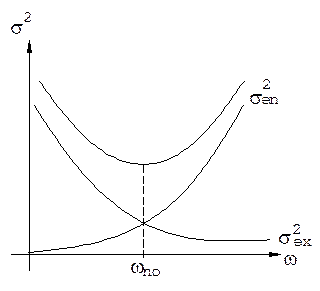
Вторая составляющая ошибки зависит от той части спектральной плотности помехи, которая совпадает с полосой пропускания системы. С расширением полосы пропускания ошибка из-за действия помехи увеличивается. Если продифференцировать выражение для ошибки, то получим

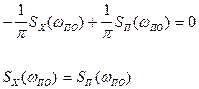
Ошибка системы определяется не только полосой пропускания, но и видом ее частотной характеристики. Поэтому в общем случае синтез системы заключается в нахождении ее оптимальных частотных характеристик из условия минимума суммарных средних ошибок при заданных статистических характеристиках сигнала и помехи.