Дифференцирующее звено.

На входе случайная функция x(f). Если случайный процесс дифференцируем, то можем записать:

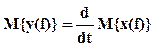
То есть математическое ожидание производной процесса равно производной его математического ожидания.

Передаточная функция такого звена равна:

W(p)=p

Спектральная плотность выходной величины может быть получена умножением спектральной плотности входной величины на w².

S₂(w)=w²S₁(w).

Интегрирующее звено.

x(f) –случайная функция.

Тогда математическое ожидание может быть записано:

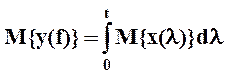
Передаточная функция идеального интегрирующего звена равна:

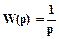. Спектральная плотность выходной величины может быть получена делением спектральной плотности входной величины на w².

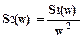
Такой процесс имеет корреляционную функцию вида:

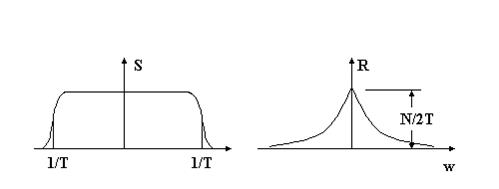
Рисунок 11‑6

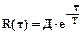
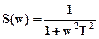. Особое место занимает гауссовский нормальный процесс.

Обычно любой случайный процесс характеризуется законом распределения своих амплитуд. Закон распределения может быть произвольным, но зачастую, в силу того, что в основном все случайные физические явления подчиняются центральной предельной теореме теории вероятностей это распределение имеет гауссовский характер:

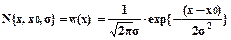
Если суммируется несколько случайных независимых явлений с произвольными законами распределения, то суммарный закон распределения стремится к гауссовскому.

11.2Средняя квадратическая ошибка системы:

Количество работы систем автоматического управления при случайных воздействиях оценивается по суммарной средней квадратической ошибке.

Для большинства случаев, когда закон распределения системы можно считать Гауссовским при расчете составляющих суммарной средней квадратической ошибки достаточно учесть математическое ожидание и корреляционную функцию ошибки или ее спектральную плотность.

На вход системы подается воздействие вида:

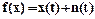
где x(t) –случайный сигнал;

n(t) – случайная помеха.

Рисунок 11‑7

Суммарная ошибка системы при этом равна:

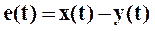
проведем преобразование Лапласа:

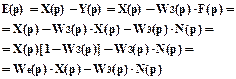
где W₃(p)-передаточная функция замкнутой системы;

W_e(p)- передаточная функция ошибки анализируемой системы.

Таким образом, суммарная ошибка состоит из двух составляющих, одна из которых зависит от передаточной функции ошибки и определяет точность воспроизведения сигнала. Вторая обусловлена действием помехи и зависит от передаточной функции замкнутой системы.

Рассмотрим ситуацию, когда сигнал и помеха являются стационарными случайными функциями. При этом будем считать математическое ожидание помехи равным нулю, а случайный сигнал представим как:

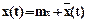
m_x - математическое ожидание сигнала;

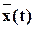- случайные составляющие сигнала.

Математическое ожидание суммарной ошибки можем записать как:

Дисперсия ошибки зависит от случайных составляющих сигнала и помехи:

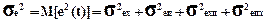
где s_e- средняя квадратическая ошибка системы;

e(t)- ошибка системы;

М – математическое ожидание от квадрата ошибки.

Первое слагаемое зависит от передаточной функции ошибки и от статистических характеристик сигнала. Оно определяет среднюю квадратическую ошибку воспроизведения сигнала x(t). Второе слагаемое зависит от передаточной функции замкнутой системы и характеристик помехи. Оно характеризует ошибку системы вследствие действия помехиn(t).

Последние два слагаемых – составляющие ошибки из-за корреляции сигнала с помехой и помехи с сигналом.

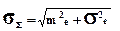
Суммарная средне квадратическая ошибка системы автоматического управления при действии на входе случайных воздействий.

На практике часто встречаются случаи, когда помеху можно считать белым шумом, тогда спектральная плотность ее в пределах полосы пропускания САУ постоянна.

Эффективная полоса пропускания системы равна:

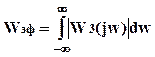
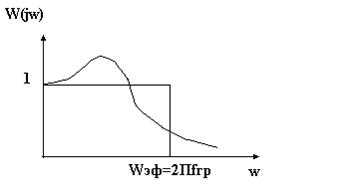
Рисунок 11‑8

w_эф –основание прямоугольника, площадь которого равна площади, ограниченной графиком АЧХ.

Помехи обычно являются белыми шумами, сигналы, как правило, не относятся к белым шумам. Однако если использовать формирующий фильтр, то анализ системы относительно сигналов сводится к случаю действия на систему белых шумов.

Формирующий фильтр – устройство, позволяющее генерировать сигнал с заданной спектральной плотностью из сигнала белого шума.

Формирующий фильтр и анализируемая система образуют некоторую расширенную систему, на вход которой действует белый шум.

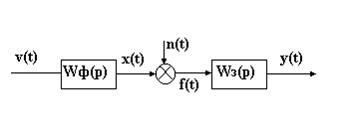
Рисунок 11‑9

Если помеха не белый шум, то в схему нужно также включить формирующий фильтр, который из белого шума будет генерировать случайную помеху с заданной спектральной плотностью.