Лекция №11. Полигауссовы модели случайных воздействий и методы их анализа.

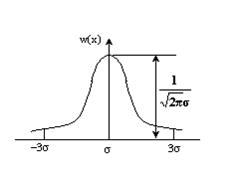
Рисунок 11‑1

Точка перегиба, в которой кривая распределения имеет максимальную крутизну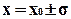

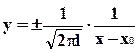Случайный гауссовский процесс имеет очень важное свойство: при прохождении через линейные цепи форма распределения не изменяться, а могут изменяться только его параметры.

А поскольку в автоматике и системах автоматического управления линейные цепи являются основными, то и аппарат гауссовский распределений адекватен задаче курса. В последнее время при более точном анализе случайных процессов было выявлено много примеров, когда случайный процесс не является Гауссовским, а имеет произвольную форму. В этом случае прибегают к аппарату полигауссовых законов распределений. Случайный процесс называют полигауссовским, если соответствующая функция распределения вероятностей представляется смесью полигауссовых законов распределения.

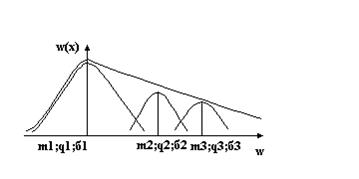
Рисунок 11‑2

При анализе линейных цепей полигауссовский закон распределения позволяет произвольно аппроксимировать смесью гауссовских, провести схему для каждой компоненты гауссовского закона, а в итоге отклики по каждой компоненте сложить и получить результирующий отклик линейной системы на произвольное распределение.

Реализацию случайного процесса с полигауссовским распределением можно представить в виде:

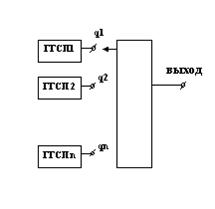
Рисунок 11‑3

Марковские модели случайных процессов .

Случайный процесс, который описывается совместным распределением двух от счетов, называется Марковским.

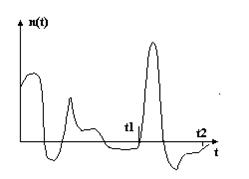
Рисунок 11‑4

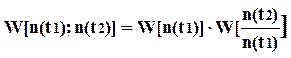
Марковские случайные процессы играют такую же роль, как и гауссовские процессы, находят широкое применение в теории случайных явлений.

Взаимоотношения между Марковскими, гауссовыми и полигауссовыми случайными процессами представляется на диаграмме случайных процессов:

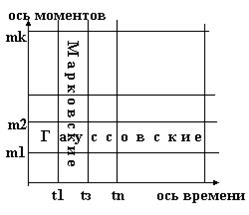
Рисунок 11‑5

Ось моментов - число начальных моментных функций, которое может быть использовано для описания того или иного случайного процесса.

Гауссовским процессам на этой диаграмме соответствует пара горизонтальных прямых, показывающих, что гауссовская модель описывается двумя первыми моментами для любого множества точек на оси времени.

Марковские процессы представлены также парами, но уже вертикальных прямых. Для любых двух точек на оси времени определяется любое множество моментов.

Рассмотрим несколько пример прохождения случайных процессов через типовые линейные звенья.